Regresión de Soporte Vectorial (Support Vector Regression – SVR)

Support Vector Regression es una variante del modelo de análisis Support Vector Machine utilizado para clasificar, sin embargo, con esta variante el modelo de vector soporte se utiliza como un esquema de regresión para predecir valores.

Máquina de Soporte Vectorial (SVM)

Es un conjunto de algoritmos de aprendizaje supervisado relacionados directamente con problemas de clasificación y regresión en donde a partir de un conjunto de datos de entrenamiento o muestras y con las clases etiquetadas se entrena una SVM para construir el modelo que prediga la clase de una muestra nueva.

Intuitivamente la SVM es un modelo que representa a los puntos de la muestra en el espacio, separando las clases en dos espacios lo más amplios posibles mediante un hiperplano de separación, el cual es definido como el vector entre los dos puntos de las dos clases más cercanas y a este vector se le llama vector soporte.

Cuando una nueva muestra se pone en correspondencia con dicho modelo, en función del espacio al que pertenece, entonces puede ser clasificada a una u otra clase. Una buena separación entre las clases permitirá una clasificación correcta.

En este sentido, una SVM construye un hiperplano o un conjunto de hiperplanos en un espacio de dimensionalidad muy alta o incluso infinita que puede ser utilizado en problemas de clasificación o regresión.

Los modelos basados en SVM están relacionados con las redes neuronales. Utilizando una función kernel, se obtiene un método de entrenamiento alternativo para clasificadores polinomiales, función de base radial y perceptrón multicapa.

Como en la mayoría de los métodos de clasificación supervisada, los datos de entrada son vistos como un vector p-dimensional (una lista ordenada de p números). La SVM busca un hiperplano que separe de forma óptima a los puntos de una clase con respecto a otra, que previamente han podido ser proyectados en un espacio de dimensionalidad superior.

En este concepto de separación óptima es donde reside la característica fundamental de las SVM, buscando que el hiperplano tenga la máxima distancia con los puntos más cercano a el. De esta manera los puntos del vector que están de un lado del hiperplano se etiquetan con una categoría y los que se encuentran del otro lado, se etiquetan con otra categoría.

A la variable predictora se le llama atributo y a los atributos utilizados para definir el hiperplano se les llaman características. La elección de la representación más adecuada del universo estudiado se lleva a cabo mediante un proceso llamado selección de características. Al vector formado por los puntos más cercanos al hiperplano se le llama vector soporte.

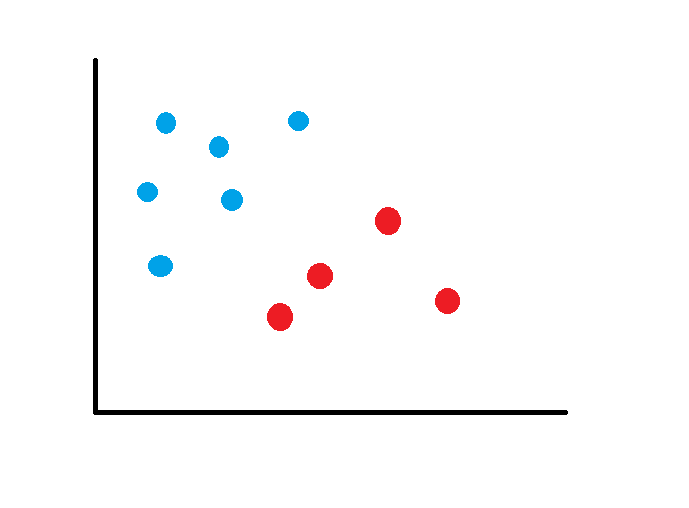
El SVM escogerá un hiperplano para separar los grupos, con la mayor distancia posible:

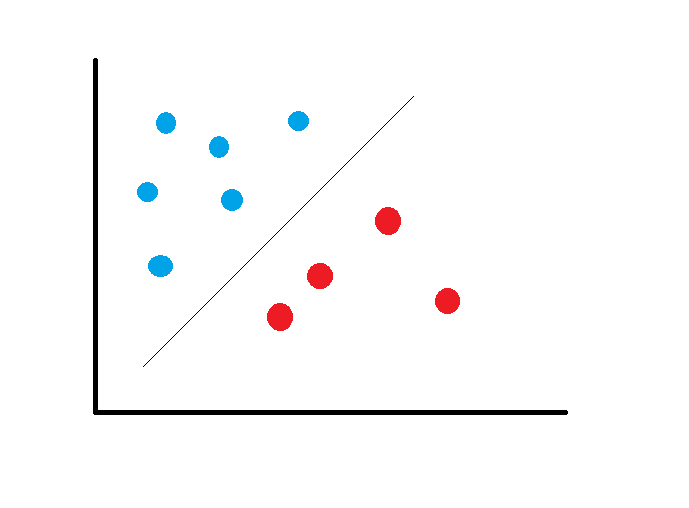
Un buen margen es aquel en el cual se tiene la máxima distancia desde los vectores de soporte hacia las dos clases.

Cuando el conjunto de datos es más complejo, el SVM convierte los datos en un espacio lineal utilizando algunas ecuaciones para llegar a un espacio dimensional más alto, utiliza por ejemplo: z = x² + y²

Support Vector Regression

Support Vector Regression utiliza el mismo principio con algunos cambios menores. En principio dado que la salida es un número real, se vuelve difícil predecir la información a mano dado que existen posibilidades infinitas. Para el caso de la regresión, entonces se establece un margen de tolerancia (epsilon) cerca del vector con el fin de minimizar el error tomando en cuenta que parte de ese error es tolerado.

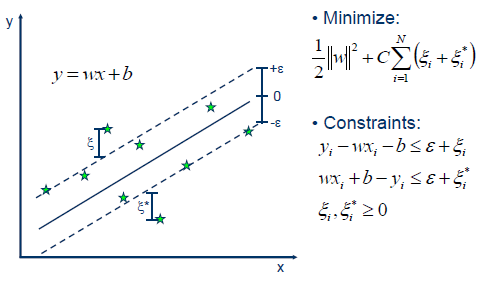
Para el caso de un problema lineal, el SVR esta dado por

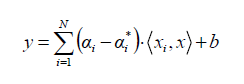
Cuando el problema no es lineal, la función Kernel transforma los datos en una característica de espacio dimensional más alto para hacer posible ejecutar la separación lineal:

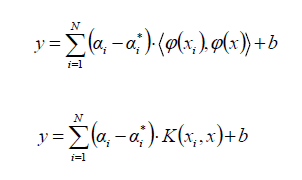
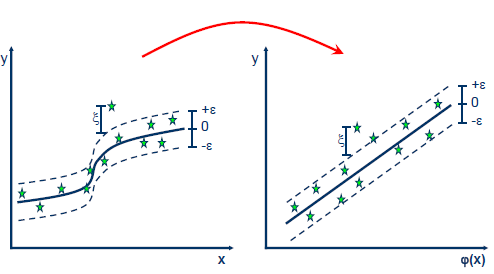
Las funciones Kernel más comunes son:

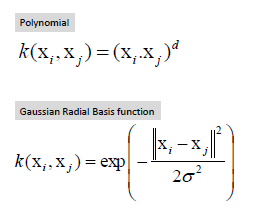
SVR – Support Vector Regression con Python

Importamos la librerías básicas y cargamos el conjunto de datos que utilizaremos para este ejemplo:

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

dataset = pd.read_csv('Salario_por_Posicion.csv')
X = dataset.iloc[:, 1:2].values
y = dataset.iloc[:, 2].values

El conjunto de datos contiene 3 columnas, de las cuales utilizaremos la segunda columna que representa el nivel del puesto de una persona, como la variable independiente y el salario que es la última columna como la variable dependiente a predecir

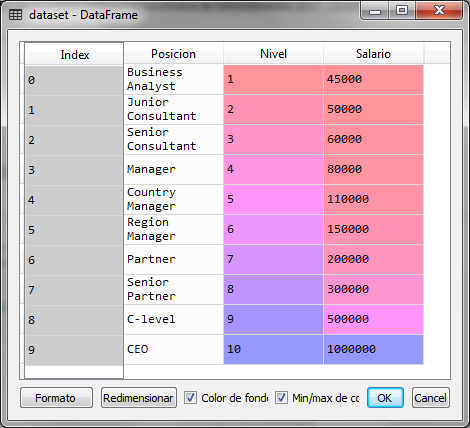
Ahora realizamos un ajuste de escalas a través de la estandarización de datos:

# Ajustes de escalas
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
sc_y = StandardScaler()
X = sc_X.fit_transform(X)
y = sc_y.fit_transform(y)

Los datos quedan ahora de la siguiente manera para la variable independiente X y la variable dependiente Y

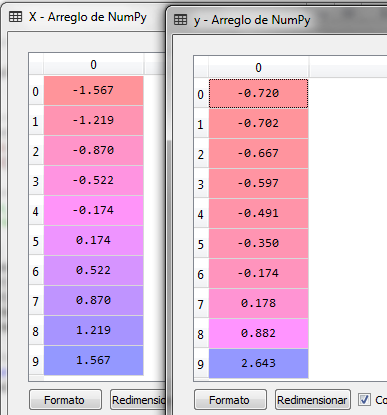
El siguiente paso es crear el objeto SVR desde la librería sklearn y el subpaquete SVM para entrenarlo con los datos X y Y utilizando la función kernel RBF

from sklearn.svm import SVR
regressor = SVR(kernel = 'rbf')
regressor.fit(X, y)

La salida obtenida después de ejecutar el bloque anterior es:

SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma='auto', kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

Para las funciones kernel tenemos varias opciones: linear, poly, rbf, sigmoid o precomputed. la funcion rbf es la función de base radial comúnmente utilizada para  el entrenamiento de algoritmos.

Ya con el modelo entrenado, podemos realizar una predicción, para el valor de X (Nivel), por ejemplo 6.5, para ello primero transformamos el valor con el objeto StandarScaler y lo enviamos al método predict(), el resultado lo transformamos a la inversa para obtener el valor del salario calculado:

# prediccion de un nuevo valor
x_trans = sc_X.transform([[6.5]])
y_pred = regressor.predict(x_trans)
y_pred = sc_y.inverse_transform(y_pred)

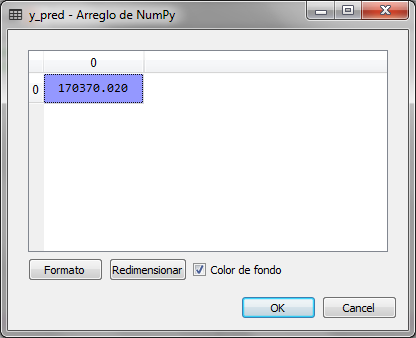
El valor de y_pred es 170,370.02 que es el salario calculado para el nivel 6.5, observamos en la tabla original que el salario para el nivel 6 es de 150,000 y para el nivel 7 es de 200,000, por lo que el valor de 170 mil esta en el espacio de predicción

Ahora graficamos los valores reales de x y Y con rojo y la linea de la predicción con azul para observar la curva y los valores calculados con la predicción del SVR

#Graficando los valores reales
x_real = sc_X.inverse_transform(X)
y_real = sc_y.inverse_transform(y)

X_grid = np.arange(min(x_real), max(x_real), 0.01) 
X_grid = X_grid.reshape((len(X_grid), 1))

x_grid_transform = sc_X.transform(X_grid)

y_grid = regressor.predict(x_grid_transform)
y_grid_real = sc_y.inverse_transform(y_grid)

plt.scatter(x_real, y_real, color = 'red')
plt.plot(X_grid, y_grid_real, color = 'blue')
plt.title('SVR')
plt.xlabel('Nivel Salarial')
plt.ylabel('Salario')
plt.show()

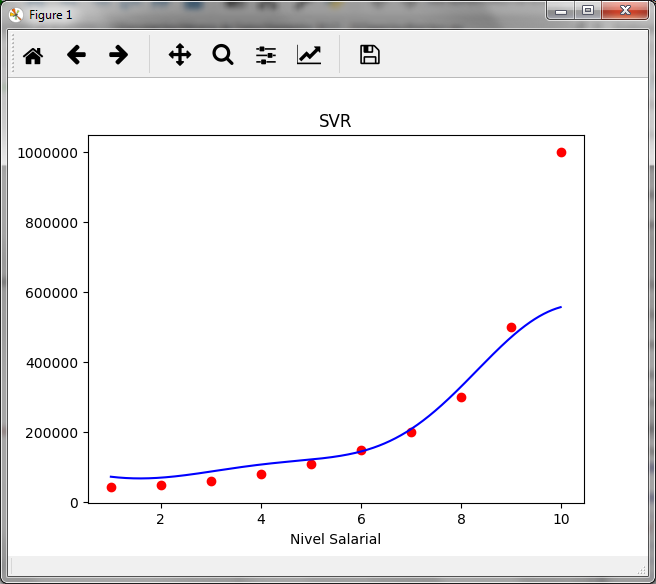
Puedes comparar el resultado con lo que se muestra en el artículo sobre los árboles de regresión y observar la diferencia, en este caso no es un clasificación para asignar el valor a un grupo, sino una interpolación.