Regresión Logística

La regresión logística es un método de clasificación, que a diferencia de la regresión simple, donde se predice un número continuo, la regresión logística se utiliza para predecir una categoría.

La clasificación tiene una amplia gama de aplicaciones que van desde el diagnóstico médico hasta incluso el marketing. Entre los modelos de clasificación podemos hablar de modelos lineales y no lineales

Modelos de clasificación lineal

• Regresión logística
• SVM (Support Vector Machine)
• Naive Bayes

Modelos de clasificación no lineal

• Árboles de decisión
• K-NN (K-Nearest Neighbors)
• Kernel SVM
• Random Forest

Cuando una variable objetivo toma sólo dos valores Si o No, ‘0’ o ‘1’, entonces el problema de clasificación se conoce como un problema de clasificación binaria y la forma efectiva de tratar con este tipo de problemas es utilizando la regresión logística.

Normalmente la función de regresión lineal toma valores de una linea recta, siendo esta función del tipo: f(x) = b₀ + b₁x   y para la regresión múltiple f(x) = b₀ + b₁x₁ + … + b_nx_n

Para el problema de clasificación ‘0’, ‘1’ podemos insertar   z = m^Tx en la función logística la cual se conoce como la función sigmoid expresada de la siguiente forma:

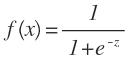
La función mapea un número real al intervalo [0,1] y es utilizada para transformar cualquier función de valor arbitrario en una función que se ajusta mejor a la clasificación.

la función f(x) representa la probabilidad P(y=1 | x;m) por lo que la regresión logística es un tipo de clasificación probabilística utilizada para representar una respuesta binaria de un predictor binario.

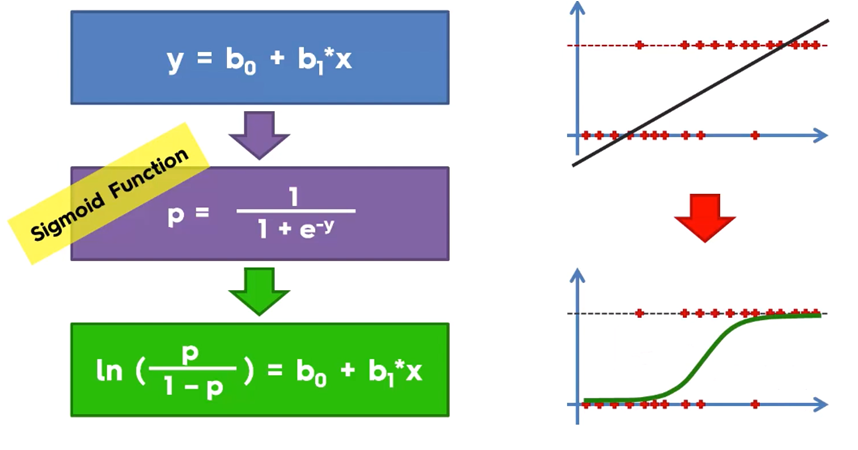
Sobre la curva de la función sigmoid tendremos el valor de la probabilidad para Y, sin embargo para la clasificación binaria, lo que se requiere es una frontera de decisión, que es una curva que separa el área donde y=0 del área donde y=1 para obtener la clasificación 0 o 1, por lo que la salida de transforma con:

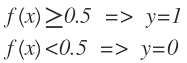
Si el valor estimado es menor a 0.5 la salida será 0 y si el valor estimado es mayor o igual a 0.5 entonces la salida de la función sigmoid será 1.

---

Logistic Regression with Python

Para este ejemplo de la regresión logística con python utilizaremos un archivo de datos que contiene información de clientes que compran o no ciertos productos en línea, para ello contamos con información sobre el género, la edad y el salario estimado, clasificando a los clientes con 0 y 1 si no compró o si compró respectivamente.

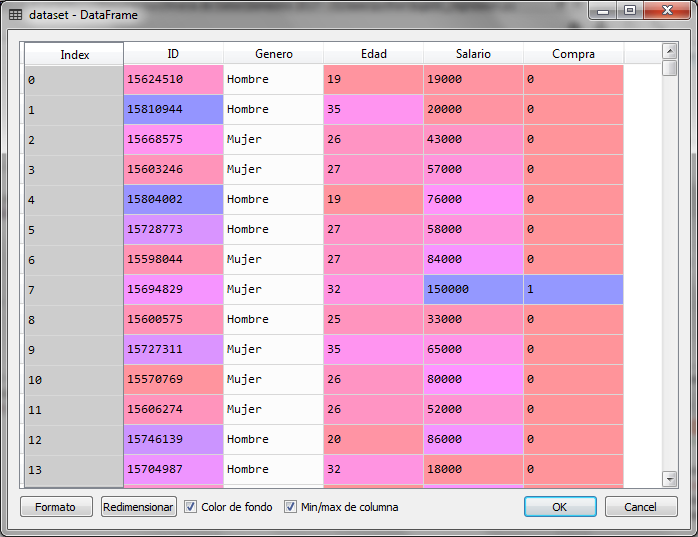
Cargamos la librerías y el conjunto de datos desde el archivo con:

# Regresion Logistica

# Importacion de librerias
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importacion del dataset
dataset = pd.read_csv('Compras_en_Linea.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

Para la variable independiente x, utilizamos la edad y el salario, columnas 2 y 3, la variable dependiente Y es la columna 4 con la información de si compró o no.

Utilizamos el 25% de los datos que contiene el archivo para pruebas y el 75% para el conjunto de entrenamiento. El archivo completo contiene 400 registros de clientes, por lo que se utilizarán 300 para el entrenamiento y 100 para las pruebas.

# Division del conjunto de datos en datos de entrenamiento
# y datos de prueba
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, 
                                                    y, 
                                                    test_size = 0.25, 
                                                    random_state = 0)

Ahora, dado que el valor de la edad y el salario se encuentran en distintas escalas, realizamos un ajuste de escalas con la clase StandarScaler

# Ajuste de escalas
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

Ahora creamos el modelo con la clase LogisticRegression de la librería sklearn y lo entrenamos con los datos del conjunto de entrenamiento X_train.

# Ajuste de la regresion logistica al conjunto de entrenamiento
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

Una vez entrenado el modelo podemos realizar la predicción de los datos contenidos en el conjunto de pruebas X_test

# Prediccion de conjunto de pruebas
y_pred = classifier.predict(X_test)

y_pred contiene los datos calculados o predecidos por el modelo de regresión logística, por lo que podemos comprar y_test con y_pred

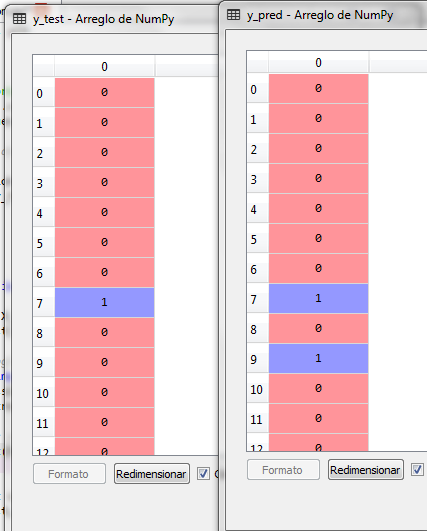
Observamos que en el renglón 9 hubo un error en la predicción, por loq ue podemos genera la matriz de confusión para analizar tanto los falsos positivos, como los falsos negativos.

# Matriz de Confusion
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

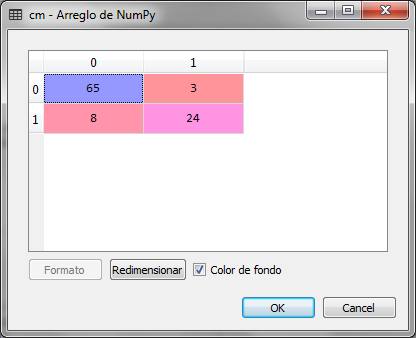
Observamos que de los 100 registros que contiene el conjunto de prueba, 8 registros que deberían de ser 1 fueron clasificados como 0 y 3 registros que deberían de ser 0 fueron clasificados como 1. Los resultados son aceptables, sin embargo para conseguir mejores resultados en la clasificación requerimos de más datos para entrenar el modelo.

La clasificación de los clientes que pertenecen al conjunto de pruebas se lleva a cabo para determinar si el cliente compra o no compra. Este conjunto contiene registros desconocidos para el modelo dado que no pertenecen al conjunto de entrenamiento y fueron separados con la función train_test_split de forma aleatoria.

Para tener una visión más clara de los resultados podemos graficar los datos tanto del conjunto de prueba como del conjunto de entrenamiento. En nuestro caso sólo lo haremos para el conjunto de entrenamiento de la siguiente manera:

# Visualizacion de los resultados de Prueba
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Regresion Logistica (Conjunto de Prueba)')
plt.xlabel('Edad')
plt.ylabel('Salario Estimado')
plt.legend()
plt.show()

La gráfica que obtenemos es la siguiente:

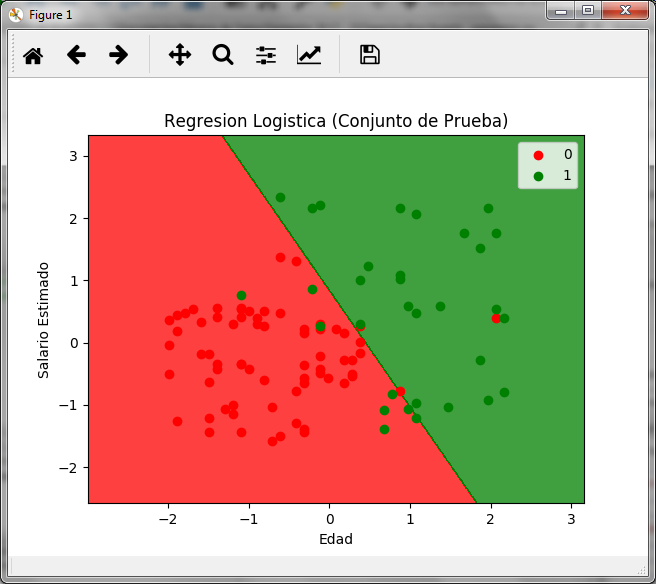
En la gráfica podemos observar las dos regiones, roja para los clientes que no compran con el valor de y=0 y verde para los clientes que si compran con el valor de y=1, en ella podemos observar también los 8 puntos verdes sobre la zona roja y los 3 puntos rojos sobre la zona verde.

Dado que de 100 registros del conjunto de prueba 11 fueron clasificados erróneamente, podemos concluir que para este caso, la precisión del  modelo es del 89%

#la precisión del modelo la obtenemos con el score
score_test =classifier.score(X_test, y_test)

El valor de la variable score_test es 0.89000 lo que significa el 89% de precisión en la clasificación y/o predicción.