Regresión Lineal con Python
Introducción a la Regresión Lineal
La regresión lineal es uno de los métodos analíticos o de inferencia, donde alguna de las variables destaca como dependiente principal en relación al resto de las variables, es decir, la variable dependiente está definida o explicada por las demás variables independientes.
La relación que existe entre la variable dependiente y las variables independientes podría estar ligada a una posible ecuación o modelo que las liga, principalmente cuando todas las variables son cuantitativas. De esta forma, se podrá llegar a predecir el valor de la variable dependiente conociendo el perfil de todas las demás.
Si la variable dependiente es cualitativa dicotómica, es decir, (0, 1) o (Si, No), entonces la regresión lineal podría utilizarse como clasificadora. Si la variable dependiente cualitativa constatara la asignación de cada elemento en grupos definidos previamente, dos o más, se puede utilizar para clasificar nuevos casos y convertirlo en el análisis discriminante.
Por otro lado, si la variable dependiente es cualitativa y las variables independientes son cuantitativas, se trata de un modelo de análisis de la varianza. Pero si la variable dependiente es cualitativa o cuantitativa y las variables independientes son cualitativas, entonces es un caso de segmentación.
En la regresión lineal tanto las variables independientes como la variable dependiente son cuantitativas y el modelo lineal viene dado por la ecuación:
Donde b1, b2, .. bn son los coeficientes o parámetros que denotan la magnitud del efecto que las variables independientes x1, x2, … xn tienen sobre la variable independiente y.
El coeficiente b0 es el término constante o o independiente del modelo. y u es el termino que representa al error del modelo.
Ahora, si se dispone de un conjunto de observaciones para cada una de las variables independientes y dependiente, ¿Cómo podemos entonces conocer los valores numéricos de los parámetros b0, b1, .. bn basados en los datos de las variables? Esto es conocido como estimación de los parámetros del modelo y una vez obtenidos estos valores, se podrá realizar una predicción del comportamiento futuro de la variable y.
Por ejemplo si tenemos un un caso hipotético donde creamos un cuadro con información sobre las ventas en periodos pasados, basados en el gasto en publicidad, la cantidad de prospectos interesados y cantidad de cotizaciones realizadas en cada periodo, podríamos inferir las ventas para periodos posteriores:
| Prospectos | Publicidad | Cotizaciones | Ventas |
| 300 | 5,000.00 | 100 | 50,000.00 |
| 400 | 4,500.00 | 120 | 45,000.00 |
| 200 | 7,000.00 | 90 | 30,000.00 |
| 800 | 7,000.00 | 350 | 90,000.00 |
| 600 | 7,500.00 | 220 | 75,000.00 |
| 650 | 4,800.00 | 300 | 81,000.00 |
| 180 | 3,000.00 | 100 | 28,000.00 |
| 700 | 6,500.00 | 400 | 128,000.00 |
| 700 | 5,400.00 | 300 | 89,000.00 |
Prospectos (x1), publicidad (x2) y cotizaciones (x3) son las variables independientes de 9 casos y ventas es la variable dependiente de esos mismo 9 casos u observaciones.
Utilizando la regresión lineal podríamos calcular las ventas que se tendrían si hubiera 900 prospectos, un gasto en publicidad de 10,000 y la realización de 500 cotizaciones. Para ello podríamos aplicar el modelo, por lo que sería necesario saber cuales son los valores de los parámetros b1, b2 y b3 principalmente.
Regresión Lineal Simple
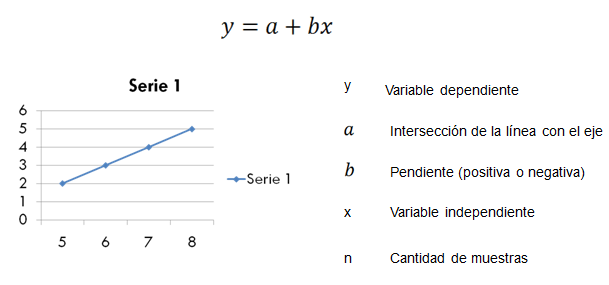
En el caso de la regresión lineal simple, el modelo sólo tendría un coeficiente, dado que sólo habría una variable independiente, como en la siguiente ecuación:
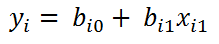
donde i = 1 .. n y n es el total de casos u observaciones
al despejar b0 tenemos la ecuación:
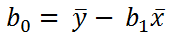
donde y(media) es el promedio de valores de la variable dependiente para todos los casos y x(media) es el promedio de los valores de la variable independiente para todos los casos
Al despejar b1 para todos los casos tenemos que el valor de b1 esta dado por:
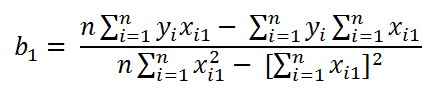
Una vez calculados los coeficientes de la ecuación, podemos calcular y para nuevos valores de x con lo que estaremos haciendo una predicción.
En resumen la regresión lineal simple la podemos ver de la siguiente manera:
Podemos calcular cualquier valor de y para valores de x que no se encuentren en el conjunto de datos actuales y que utilizamos como conjunto de entrenamiento, es decir, para el calculo de los coeficientes de la ecuación.
Python
Para el ejemplo con python, vamos a considerar la siguiente tabla de datos:
| Años de experiencia | Salario |
| 1.1 | 39,343.00 |
| 1.3 | 46,205.00 |
| 1.5 | 37,731.00 |
| 2 | 43,525.00 |
| 2.2 | 39,891.00 |
| 2.9 | 56,642.00 |
| 3 | 60,150.00 |
| 3.2 | 54,445.00 |
| 3.2 | 64,445.00 |
| 3.7 | 57,189.00 |
| 3.9 | 63,218.00 |
| 4 | 55,794.00 |
| 4 | 56,957.00 |
| 4.1 | 57,081.00 |
| 4.5 | 61,111.00 |
| 4.9 | 67,938.00 |
| 5.1 | 66,029.00 |
| 5.3 | 83,088.00 |
| 5.9 | 81,363.00 |
| 6 | 93,940.00 |
| 6.8 | 91,738.00 |
| 7.1 | 98,273.00 |
| 7.9 | 101,302.00 |
| 8.2 | 113,812.00 |
| 8.7 | 109,431.00 |
| 9 | 105,582.00 |
| 9.5 | 116,969.00 |
| 9.6 | 112,635.00 |
| 10.3 | 122,391.00 |
| 10.5 | 121,872.00 |
Donde la variable independiente X representa los años de experiencia y la variable dependiente Y el salario. Guardamos estos datos en un archivo de texto separado por comas como CSV utilizando Excel y le ponemos el nombre Salary_Data.csv
Lo primero que haremos es importar las librerías que vamos a requerir:
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd
numpy es un paquete fundamental para el cómputo científico con python debido a que contiene objetos y funciones para realizar operaciones con arreglos multidimensionales, herramientas para integrar código fortran y C/C++, soporte para el álgebra lineal, transformada de Fourier y la capacidad de generar números aleatorios.
matplotlib contiene las herramientas, funciones y objetos para crear gráficos
pandas es la librearía para manipular estructuras de datos, es una extensión de numpy que también permite la manipulación de archivos externos de datos.
Por lo que el siguiente paso es cargar el archivo Salary_Data.csv utilizando la librería pandas y separar las variables dependientes e independientes:
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Salary_Data.csv') x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values
Una vez creadas las variables independientes y dependientes con los datos de los años de experiencia y el salario, vamos a dividir ambos vectores en dos vectores cada uno. El primero con con datos aleatorias extraídos de la variable independiente (años de experiencia) para crear un conjunto de datos para entrenar el modelo, es decir, para calcular los coeficientes a y b (o b0 y b1), al cual le llamamos el conjunto de entrenamiento y el segundo para probar el modelo, por lo que le llamamos el conjunto de prueba.
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Salary_Data.csv') x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values #dividimos los datos en el conjunto de entrenamiento y el conjunto de pruebas from sklearn.cross_validation import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/3, random_state=0)
De la librería Sci-Kit Learn (sklearn) importamos la función train_test_split para dividir los datos. En la función utilizamos las variables x y y más dos parámetros adicionales: test_size y random_state. Con el primero (test_size) indicamos que el tamaño para el conjunto de prueba, guardados en las variables x_test y y_test tendrán un tercio del conjunto total, es decir 10 registros, dado que el conjunto total es de 30 y los 10 seleccionados estarán escogidos de manera aleatoria de entre esos 30, dado que el último parámetro de la función es random_state=0.
El siguiente paso es cargar el conjunto de entrenamiento al modelo de regresión lineal para calcular los coeficientes, es decir, entrenar al modelo.
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Salary_Data.csv') x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values #dividimos los datos en el conjunto de entrenamiento y el conjunto de pruebas from sklearn.cross_validation import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/3, random_state=0) #Cargamos el conjunto de entrenamiento al modelo de Regresión Lineal from sklearn.linear_model import LinearRegression regressor = LinearRegression() regresor.fit(x_train, y_train)
De la misma librería sklearn en el subpaquete linear_model importamos la clase LinearRegression y creamos el objeto regressor con el constructor de la clase.
Una vez creado el objeto, invocamos el método fit() proporcionándole los datos de entrenamiento.
Ya con el modelo entrenado, podemos ahora predecir los valores de Y con el conjunto de pruebas x_test y comparar con los valores reales y_test.
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Salary_Data.csv') x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values #dividimos los datos en el conjunto de entrenamiento y el conjunto de pruebas from sklearn.cross_validation import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/3, random_state=0) #Cargamos el conjunto de entrenamiento al modelo de Regresión Lineal from sklearn.linear_model import LinearRegression regressor = LinearRegression() regressor.fit(x_train, y_train) #Predicción de los resultados del conjunto de pruebas (x_test) y_pred = regressor.predict(x_test) #Ahora comparamos y_pred con los valores reales y_test
Ahora que ya tenemos los valores calculados con el modelo de la regresión lineal, podemos compararlos contra los valores reales (y_pred vs y_test) mostrando una gráfica.
#Regresion Lineal Simple import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Salary_Data.csv') x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values #dividimos los datos en el conjunto de entrenamiento y el conjunto de pruebas from sklearn.cross_validation import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/3, random_state=0) #Cargamos el conjunto de entrenamiento al modelo de Regresión Lineal from sklearn.linear_model import LinearRegression regressor = LinearRegression() regressor.fit(x_train, y_train) #Predicción de los resultados del conjunto de pruebas (x_test) y_pred = regressor.predict(x_test) #Ahora comparamos y_pred con los valores reales y_test plt.scatter(x_test, y_test, color = 'red') plt.plot(x_train, y_pred, color = 'blue') plt.title('Salario vs Experiencia (Conjunto de prueba)') plt.xlabel('Años de Experiencia') plt.ylabel('Salario') plt.show()
Con puntos rojos se muestran los valores reales para Y del conjunto de prueba y la recta azul muestra la linea de regresión calculada para los valores predecidos.
Los valores de ambos vectores son los siguientes:
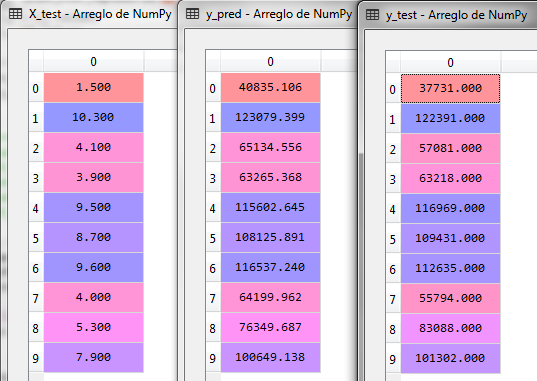
La tabla del lado izquierdo muestra los años de experiencia (x_test), para los 10 valores del conjunto de prueba, la tabla de en medio y_test es el salario original correspondiente a los años de experiencia. En la tabla de la extrema derecha se muestran los valores calculados con el modelo de regresión lineal para el salario correspondiente a los años de experiencia.
Por ejemplo, en el segundo renglón menciona que con 10.3 años de experiencia el salario actual es de 123,079.39 y la predicción indica un salario de 122,391.00 la diferencia es de 688.39
Podemos observar que los valores son distintos, pero no muy alejados de la realidad. El error es mínimo y puede aceptarse el resultado de la regresión para valores desconocidos de x.
Recomendaciones
Para iniciar con la programación en python, este curso de Introducción a la programación con python te puede ser muy útil. Por otro lado, en este webinar podrás conocer los detalles de arquitectura y soluciones para machine learning de Azure.
También para el desarrollo en la nube podemos utilizar Amazon Web Services, estas ligas son para el curso de certificación de Asociado y el de Profesional en diseño y arquitectura de AWS.
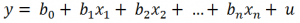

Wow, it seems interesting how can code solve those problems. What method should we use?
Hello, that’s an interesting topic to discuss. Agree with an innovation that you share through this article. Could I add some points?
Hello, you can use object oriented programming as well
Sure, what points would you add?
Muy buen ejemplo, bien explicado
Quisiera saber como poder aplicar regresion lineal para predecir la disponibilidad de playas de estacionamiento conociendo las entradas y salidas? o se necesitarian mas variables?
Hola Alex,
Que variables estas considerando? únicamente fecha y hora de entrada y salida?
Que esas variables podrías hacer la prueba, pero talvez en este caso requieras series de tiempo
Muchas Gracias, Saludos!!!
Hola! he modificado un poco tu codigo pero a la hora de graficar obtengo un error al nombrar los ejes, obtengo el siguiente error: TypeError: ‘str’ object is not callable Aqui esta el codigo completo, como podria resolver este error? te agradezco por el ejemplo y tu ayuda, saludos, Jesus import numpy as np import matplotlib.pyplot as plt import pandas as pd dataset = pd.read_csv(‘/Users/jesusjm/Data science Phyton/Salary_Data.csv’) type(dataset) dataset.head() x = dataset.iloc[:, :-1].values y = dataset.iloc[:, 1].values y from sklearn.linear_model import LinearRegression regressor = LinearRegression() regressor.fit(x, y) print(f’intercepto ‘,regressor.intercept_) print(f’pendientes ‘,regressor.coef_) ypred = regressor.predict(x) plt.scatter(x,y) plt.plot(x,ypred, color=”darkorange”) plt.title(‘hola’) plt.xlabel(‘Años… Read more »
Hola! ya resolvi el problema! gracias!
Excelente
Hola Jesús,
Perdón por la tardanza en responder, pero veo que si pudiste resolverlo. Saludos