Linear Discriminant Analysis

El análisis discriminante es una técnica predictiva de clasificación ad hoc y se denomina así por que se conocen previamente los grupos o clases antes de realizar la clasificación, que a diferencia de los árboles de decisión (post hoc) donde los grupos de clasificación se derivan de la ejecución de la técnica misma sin conocerse previamente.

Siquieres verlo en video:

Es una técnica ideal para construir un modelo predictivo y pronosticar al grupo o clase a la que pertenece una observación a partir de determinadas características que delimitan su perfil.

Como su nombre lo indica, el análisis discriminante ayuda a identificar las características que diferencian (discriminan) a dos o más grupos y a crear una función capaz de distinguir con la mayor precisión posible a los miembros de un grupo u otro.

Por otro lado, LDA tambiés es un método de reducción de dimensión, dado que tomando n variables independientes del conjunto de datos, el método estrae p <= n nuevas variables independientes que más contribuyen a la separación de clases de la variable dependiente.

la interpretación de las diferencias entre grupos consiste en determinar:

En qué medida un conjunto de características permite extraer dimensiones que diferencian a los grupos y
Cuáles de estas características son las que en mayor medida contribuyen a tales dimensiones, es decir, cuáles presentan el mayor poder de discriminación.

En resumen, podemos decir que el Análisis Discriminante Lineal – LDA tiene las siguientes aplicaciones:

Es muy utilizado como técnica de reducción de la dimensión
Es utilizado como un paso en el pre-procesamiento de datos para la clasificación de patrones
Tiene el objetivo de proyectar un conjunto de datos en un espacio de menor dimensión

El objetivo del LDA es proyectar el espacio de una característica (conjunto de datos de n dimensiones) en un subespacio pequeño k donde k <= n – 1, manteniendo la información discriminatoria de clases.

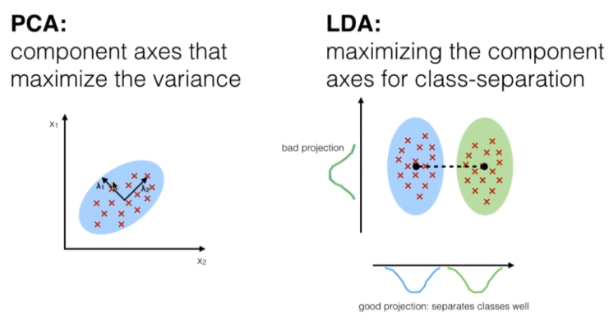
Tanto PCA (Análisis del Componente Principal) y el LDA (Análisis Discriminante Lineal) son técnicas lineales de transformación utilizadas para la reducción de la dimensión, sin embargo, PCA es no supervisado y LDA es supervisado dada su relación con la variable dependiente.

fuente: https://sebastianraschka.com/Articles/2014_python_lda.html

Los 5 pasos generales para el análisis discriminante lineal son:

Calcular los vectores medios d-dimensionales para las diferentes clases del conjunto de datos.
Calcular las matrices de dispersión (entre clases y dentro de las clases).
Calcular los vectores propios (e1, e2, …ed) y sus correspondientes valores propios (l1, l2, …, ld) para las matrices de dispersión
Ordenar los vectores propios de forma decreciente en relación a los valores propios y seleccionar lo k vectores propios con los valores propios más grandes para formar una matriz de dimensión d x k llamada W (donde cada columna representa un vector propio).
Utilizar la matriz d x k de vectores propios para transformar las muestras en un nuevo sub espacio. Esta se puede sumarizar por la multiplicación de matrices Y = X x W (donde X es una matriz n x d que representa las n muestras y y es la transformada n x k de las muestras en el nuevo sub espacio).

Si el objetivo es reducir la dimensión de un conjunto de datos d-dimensional para proyectarlo en un sub espacio k-dimensional (donde k ˂ d), cómo saber que tamaño seleccionar para k (donde k es el número o la dimensión del nuevo sub espacio) y cómo saber si tenemos un sub espacio que representa correctamente los datos.

Calcular los vectores propios para el conjunto de datos y concentrarlos para formar las matrices de dispersión, donde cada uno de estos vectores está asociado a un valor propio el cual nos indica el tamaño o magnitud de los vectores.

Si se observa que todos los valores propios tiene magnitudes similares, entonces esto es un buen indicador de que los datos ya están proyectados a un buen sub espacio.

Pero, si alguno de los valores propios es mucho más grande que otros, lo que interesa es mantener solo aquellos vectores que tengan los valores propios más grandes, dado que ellos contiene más información relacionada con la distribución de los datos. Los valores que estén más cercarnos a cero son menos informativos y no deben tomarse para la creación del nuevo sub espacio.

Implementación de LDA con Python

Para el ejercicio con python vamos a considerar un conjunto de datos con características de tres categorías de vinos. Las características están conformadas con 13 variables que van desde el grado de alcohol, la acidez, el aroma, etc. Para conformar tres segmentos de clientes que representan las clases o grupos. En total se tiene 179 registro o muestras.

Alcohol	Malic Acid	Ash	Ash Alcanity	Magnesium	Total Phenols	Flavanoids	Nonflavanoid Phenols	Proanthocyanins	Color_Intensity	Hue	OD280	Proline	Customer Segment
14.23	1.71	2.43	15.6	127	2.8	3.06	0.28	2.29	5.64	1.04	3.92	1065	1
13.2	1.78	2.14	11.2	100	2.65	2.76	0.26	1.28	4.38	1.05	3.4	1050	1
13.16	2.36	2.67	18.6	101	2.8	3.24	0.3	2.81	5.68	1.03	3.17	1185	1
14.37	1.95	2.5	16.8	113	3.85	3.49	0.24	2.18	7.8	0.86	3.45	1480	1
13.24	2.59	2.87	21	118	2.8	2.69	0.39	1.82	4.32	1.04	2.93	735	1
14.2	1.76	2.45	15.2	112	3.27	3.39	0.34	1.97	6.75	1.05	2.85	1450	1
14.39	1.87	2.45	14.6	96	2.5	2.52	0.3	1.98	5.25	1.02	3.58	1290	1
14.06	2.15	2.61	17.6	121	2.6	2.51	0.31	1.25	5.05	1.06	3.58	1295	1
14.83	1.64	2.17	14	97	2.8	2.98	0.29	1.98	5.2	1.08	2.85	1045	1
13.86	1.35	2.27	16	98	2.98	3.15	0.22	1.85	7.22	1.01	3.55	1045	1
14.1	2.16	2.3	18	105	2.95	3.32	0.22	2.38	5.75	1.25	3.17	1510	1
14.12	1.48	2.32	16.8	95	2.2	2.43	0.26	1.57	5	1.17	2.82	1280	1
13.75	1.73	2.41	16	89	2.6	2.76	0.29	1.81	5.6	1.15	2.9	1320	1
14.75	1.73	2.39	11.4	91	3.1	3.69	0.43	2.81	5.4	1.25	2.73	1150	1

Para iniciar con el modelo, cargamos el archivo con los datos y separamos en X la variable independiente las columnas 1 a 13 y en Y la variable dependiente la columna 14 con la segmentación de clientes.

# LDA

# Importacion de librerias
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importacion del dataset
dataset = pd.read_csv('Vinos.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values

Dividimos el conjunto de datos en conjunto de entrenamiento y conjunto de pruebas para entrenar al modelo LDA, posteriormente hacemos un ajuste de escalas y creamos el modelo LDA para reducir la dimensión a 2 variables.

Para probar que con 2 de 13 variables podemos hacer una predicción o clasificación de los 3 grupos de vinos, utilizamos la regresión logística y checamos la matriz de confusión

Untitled

In [1]:

# Importacion de librerias
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

In [3]:

# Importacion del dataset
dataset = pd.read_csv('Vinos.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values

In [4]:

# Dividivmos el conjunto de datos en muestra de entrenamiento y 
# muestra de prueba
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size = 0.2, 
                                                    random_state = 0)

In [5]:

# Ajuste de Escalas
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

In [6]:

# Aplicando LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components = 2)
X_train = lda.fit_transform(X_train, y_train)
X_test = lda.transform(X_test)

In [7]:

# Comprobamos las variables independientes resultantes con 
# una regresion Logistica para determinar que con solo dos
# variables obtenemos la predicción adecuada
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

Out[7]:

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=0, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)

In [8]:

# Prediccion del conjunto de prueba para 
# comprar los resultados
y_pred = classifier.predict(X_test)

In [9]:

# Creamos la matriz de confusion
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

In [10]:

# Visualizacion de los datos de entrenamiento
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
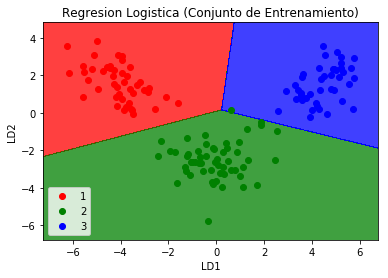
plt.title('Regresion Logistica (Conjunto de Entrenamiento)')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend()
plt.show()

In [11]:

# Visualizacion de los resultados de prueba
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
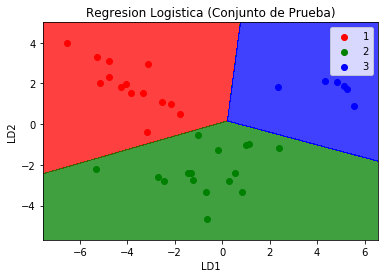
plt.title('Regresion Logistica (Conjunto de Prueba)')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend()
plt.show()

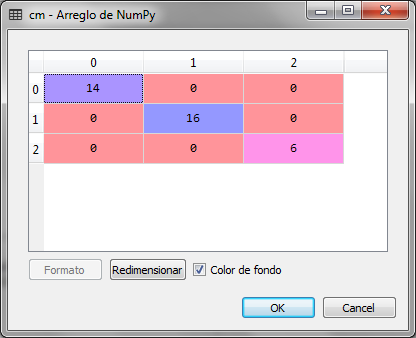
Observamos que la matriz de confusión para la predicción del grupo con la regresión logística para las nuevas variables con la dimensión reducida es muy acertada y no existen errores

0 0 votes

Article Rating

2 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

juan

5 years ago

hola hola, muy buena tu explicación, yo estoy haciendo un ejercicio usando scikit learn pero los datos que estoy usando solo son dos variables con 4 clases y usar el algoritmo de analisis lineal discriminante, podrías ayudarme?

Author

Jacob Avila Camacho

Reply to juan

Hola Juan,
Perdón por la tardanza en responder.
Si, con gusto, que necesitas en que vas?

Linear Discriminant Analysis

Linear Discriminant Analysis

Implementación de LDA con Python

JacobSoft

Tutorial Básico de Python

Implementación de WebSockets con Node.js

Cómo crear una base de datos con MongoDB y Compass