K-Vecinos más cercanos (KNN)

KNN es un método de clasificación supervisada que sirve para estimar la función de densidad:

f(x/Cj)

Don de x es la variable independiente y Cj la clase j, por lo que la función determina la probabilidad a posteriori de que la variable x pertenezca a la clase j.

En el reconocimiento de patrones, el algoritmo KNN es utilizado como método de clasificación de objetos con un entrenamiento a través de ejemplos cercanos en el espacio de diversos elementos. Cada elemento esta descrito en términos de p atributos considerando q clases para la clasificación.

Chécalo en video aquí:

El espacio de los valores de la variable independiente es particionado en regiones por localizaciones y etiquetas de los elementos de entrenamiento. De esta forma un punto en el espacio es asignado a la clase C, si ésta es la clase más frecuente entre los k elementos más cercanos.

Para determinar la cercanía de los elementos se utiliza comúnmente la distancia euclidiana:

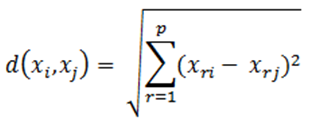
La fase de entrenamiento consiste en almacenar los vectores característicos y las etiquetas de las clases de dichos elementos de entrenamiento.

En la fase de clasificación se calcula la distancia entre los vectores almacenados y el nuevo vector y se seleccionan los k elementos más cercanos.

El nuevo vector es clasificado con la clase que más se repite en los vectores seleccionados.

Ejemplo

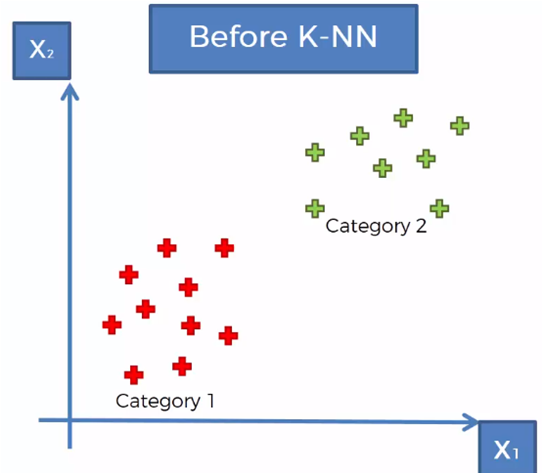
Considerando un conjunto de datos clasificados en dos categorías, como se muestra en la gráfica anterior, se requiere clasificar un nuevo vector de datos que se encuentra en la región mostrada en la siguiente gráfica.

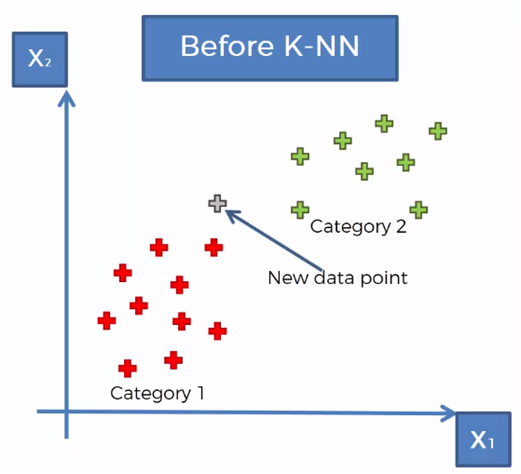
El algoritmo KNN sigue los siguientes pasos para determinar a que categoría pertenece el nuevo dato que se desea clasificar:

• Paso 1: Selecciona el número de K vecinos
• Paso 2: Toma los K vecinos más cercanos al nuevo elemento de acuerdo con la distancia euclidiana
• Paso 3: Entre los K vecinos, contar el número de elementos que pertenece a cada categoría
• Paso 4: Asignar el nuevo elemento a la categoría donde se contaron más vecinos

Tomando para el ejemplo que K = 5, marcamos los 5 vecinos más cercanos al nuevo elemento

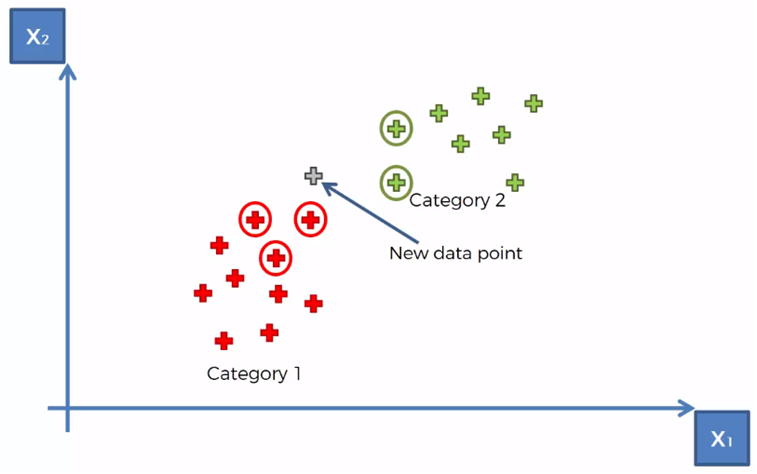
Contamos que existen 3 elementos de la categoría 1 y dos elementos de la categoría 2 de entre los 5 vecinos más cercanos

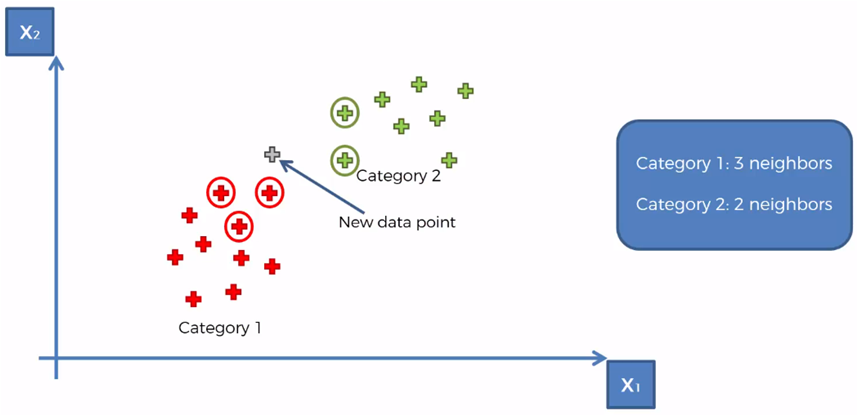
Por lo tanto, la categoría con más elementos contados es la categoría 1, por lo que el nuevo elemento se asigna a la categoría 1

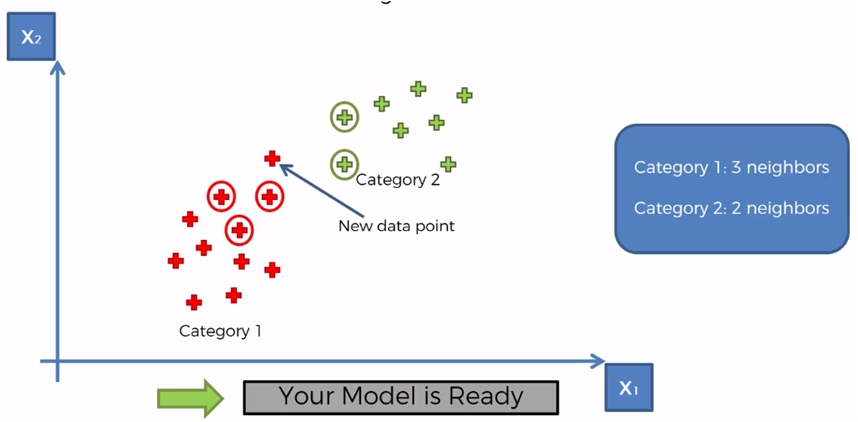
KNN con Python

Para el ejemplo con Python utilizaremos un conjunto de datos con registros de clientes que compraron y no compraron. Por lo que tenemos dos categorías: Compró = 1 y No Compro = 0.

La variable independiente esta compuesta por datos sobre el género, la edad y el salario estimado del cliente, sin embargo para el ejemplo gráfico utilizaremos sólo la edad y el salario estimado como variables independientes:

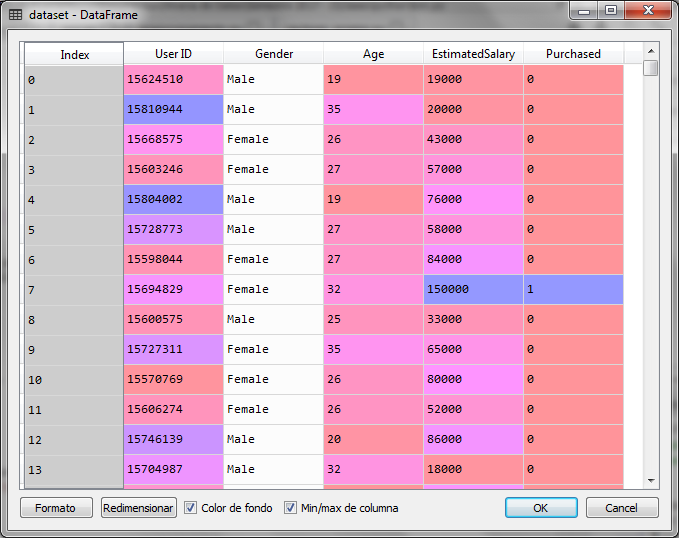
El primer paso es cargar las librerías necesarias para el modelo de machine learning y cargar el archivo de datos separando las variables independiente en X y la variable dependiente en Y

# K-Nearest Neighbors (K-NN)

# Importar librerias

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importar el dataset
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

Al ejecutar el código anterior tenemos para la variable X y Y lo siguiente:

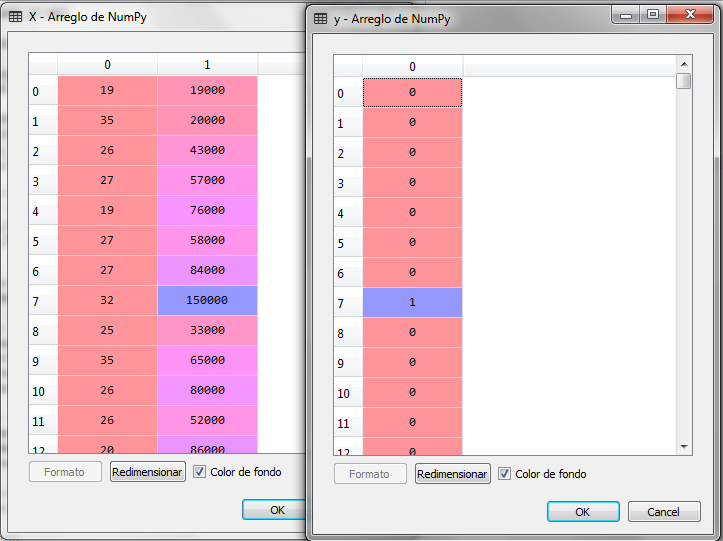
Ahora separamos los datos en con sub conjuntos, entrenamiento y prueba, dejando el 25% de los registros para prueba y el 75% para entrenamiento, posteriormente ajustamos las escalas.

# Creamos el conjunto de entrenamiento y 
# lo separamos del conjunto de prueba
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size = 0.25, 
                                                    random_state = 0)

# Ajuste de escalas
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

Después de ajustar las escalas tenemos para X_train y X_test lo siguiente:

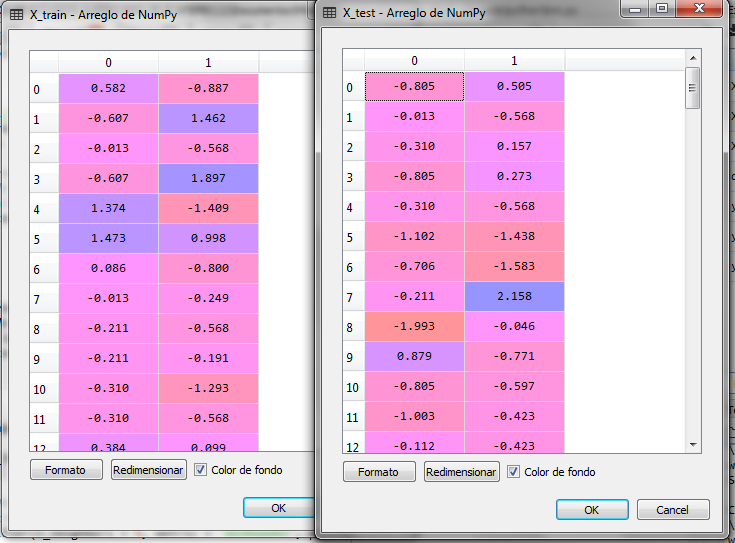
Ahora entrenamos el modelo y predecimos el conjunto X_test. El modelo para el algoritmo KNN lo obtenemos de la clase KNeighborsClassifier de la librería sklearn

# Entrenamiento del modelo KNN
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 2)
classifier.fit(X_train, y_train)

# Predicción del conjunto de prueba
y_pred = classifier.predict(X_test)

# Matriz de confusion
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

Con la métrica minkowski y p = 2 en los argumentos del constructor de la clase KNeighborsClassifier le estamos indicando que use la distancia euclidiana como método para encontrar los vecinos más cercanos.

Con la predicción del conjunto de prueba X_test nos presenta el resultado el y_pred y creamos la matriz de confusión cm

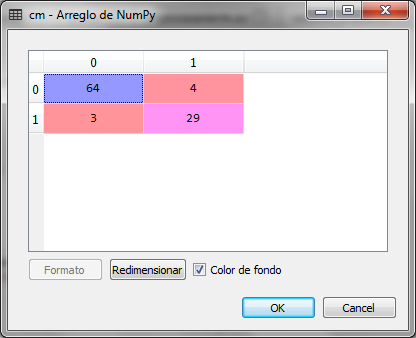
Observamos que de 100 registros del conjunto de prueba, hubo 4 falsos negativos y 3 falsos positivos que dan 7 errores, lo cual representa un 93% de precisión del modelo de clasificación para los K-vecimos más cercanos.

Si graficamos la predicción del conjunto de prueba obtenemos lo siguiente:

# Visualizacion de los datos de prueba
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('K-NN (Prueba)')
plt.xlabel('Edad')
plt.ylabel('Salario Estimado')
plt.legend()
plt.show()

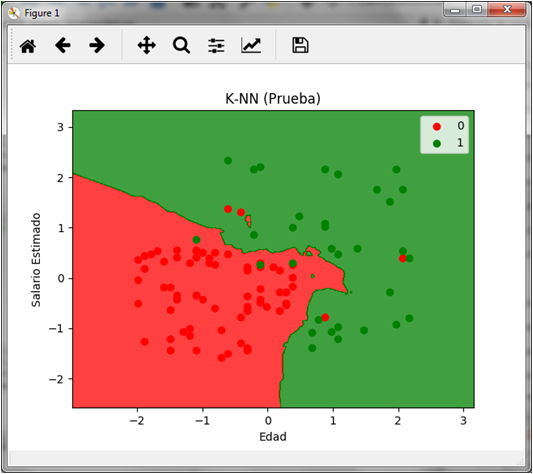
En la gráfica podemos observar los 4 puntos rojos sobre el área verde y los 3 puntos verdes sobre el área roja que representan tanto los falsos negativos como los falsos positivos respectivamente.

Comentarios finales

Para el manejo de python, este curso podría ser el indicado para iniciar con python. Adicionalmente, si te interesa ejecutar estos modelos en la nube,  este webinar gratuito de Azure te podrá servir para conocer los detalles de operación de dicha plataforma, que al igual que Amazon Web Service son esquemas de procesamiento y servicios en la nube para machine learning y otras soluciones.

Por último, para el manejo de bases de datos podemos iniciar con estos cursos tanto de diseño como de práctica de SQL.