k-Means Clustering con Python

Como se describió en el artículo anterior: Cluster Analysis, el método k-Medias es un método no jerárquico basado en centroides, robusto y fácil de implementar, en donde se requiere especificar previamente el número de grupos que se van a generar y a los cuales se van a asignar los datos.

Adicionalmente, este tipo de métodos son recomendados para grandes cantidades de datos.

Checa el tema en video

El dataset utilizado en el ejemplo lo puedes descargar de este enlace: dataset

El algoritmo funciona de la siguiente manera: supongamos que tenemos el siguiente conjunto de datos.

Al aplicar el algoritmo, deberemos obtener el siguiente resultado:

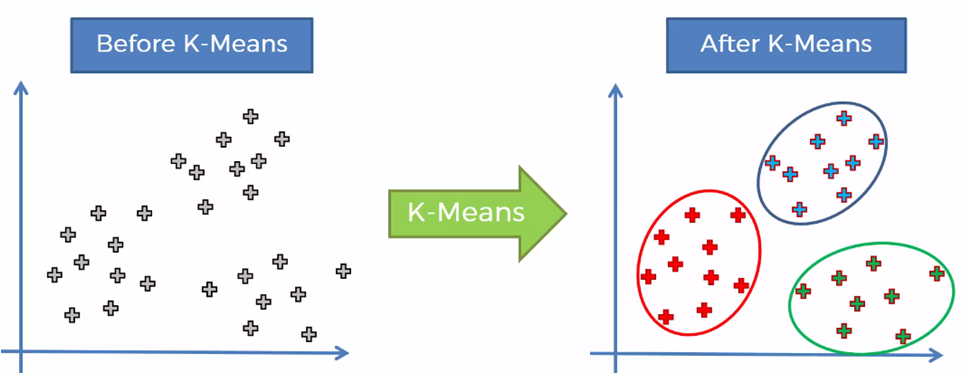
Para llegar a ello, el procedimiento que sigue el algoritmo es el siguiente:

Algoritmo k-Means
1. Seleccionar el número de k grupos (clusters)
2. Generar aleatoriamente k puntos que llamaremos centroides
3. Asignar cada elemento del conjunto de datos al centroide más cercano para formar k grupos
4. Reasignar la posición de cada centroide
5. Reasignar los elementos de datos al centroide más cercano nuevamente
   5.1 Si hubo elementos que se asignaron a un centroide distinto al original, regresar al paso 4, de lo contrario, el proceso ha terminado

Para entender de manera clara el algoritmo anterior, vayamos paso a paso describiéndolo gráficamente:

1. Seleccionar el número de k grupos

Para este conjunto de datos, digamos que k es igual a 2. (Más adelante veremos como seleccionar k).

2. Seleccionar aleatoriamente k puntos que llamaremos centroides (k = 2)

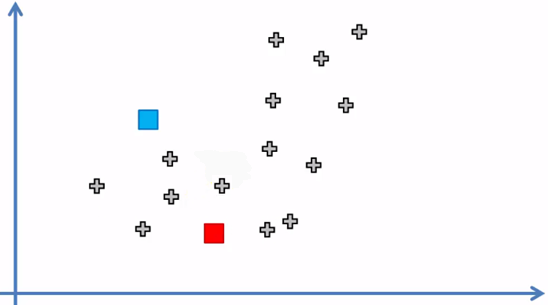
Los puntos azul y rojo representan los dos centroides ubicados aleatoriamente en el espacio del conjunto de datos.

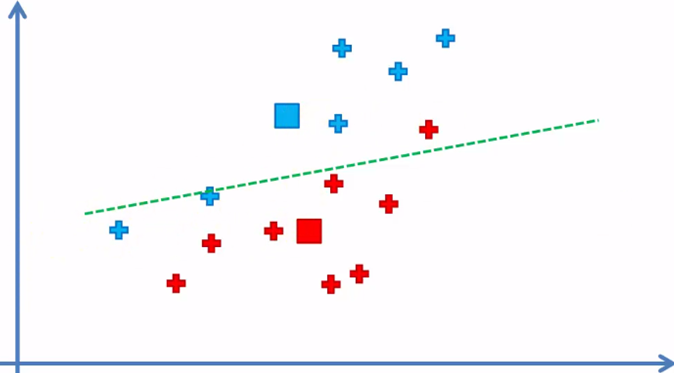
3. Asignar cada elemento del conjunto de datos al centroide más cercano para formar k = 2 grupos

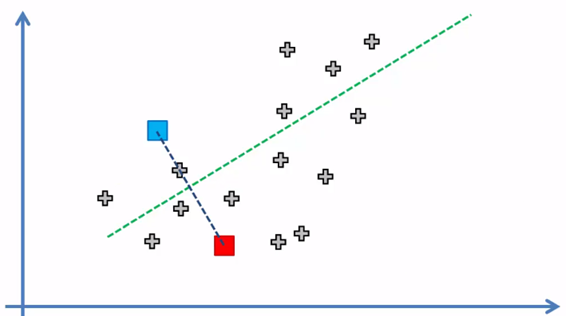
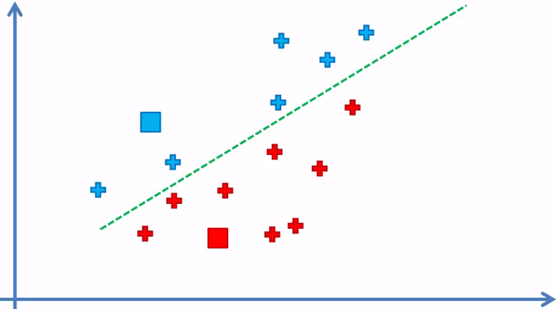
Cada elemento quedó asignado al centroide más cercano a el y de esta manera se forma los k = 2 grupos o clusters, ahora el siguiente paso:

4. Reasignar la posición de cada centroide

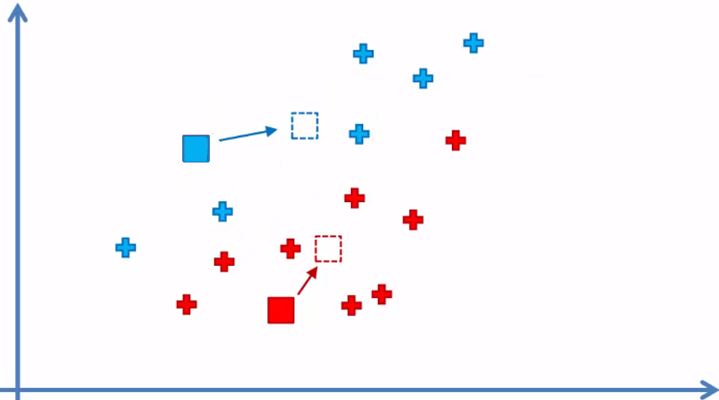
5. Reasignar los elementos de datos al centroide más cercano nuevamente

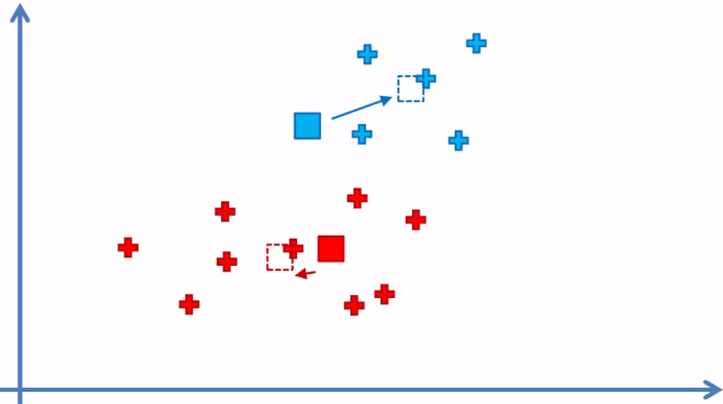
Como podemos observar, hay elementos azules que ahora están más cercanos al centroide rojo y un elemento rojo del lado de la frontera del centroide azul, por lo que esos elementos serán reasignados.

5.1 Si hubo elementos que se asignaron a un centroide distinto al original, regresamos al paso 4

Dado que si hubo elementos reasignados, volvemos al paso 4 y cambiamos la posición de los centroides

Paso 5 nuevamente y reasignamos

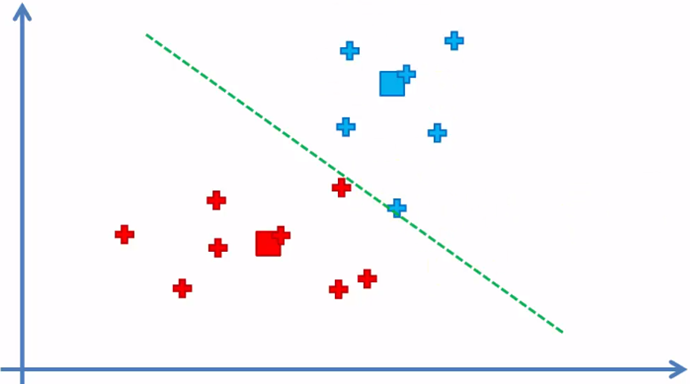
Regresamos al paso 4 nuevamente

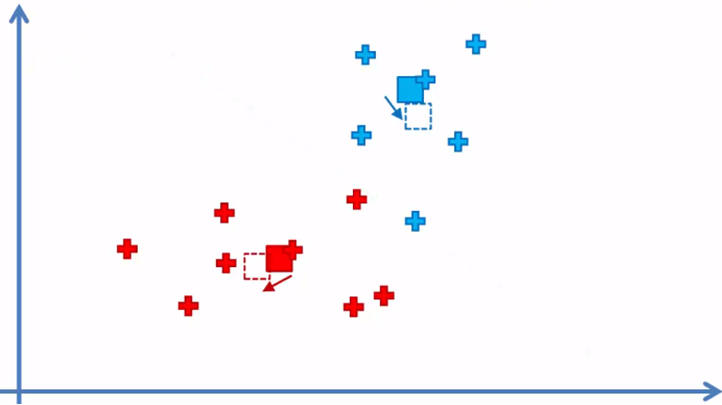
y el algoritmo continua entre el paso 4 y 5 hasta que ya no haya elementos que se tengan que reasignado de cluster

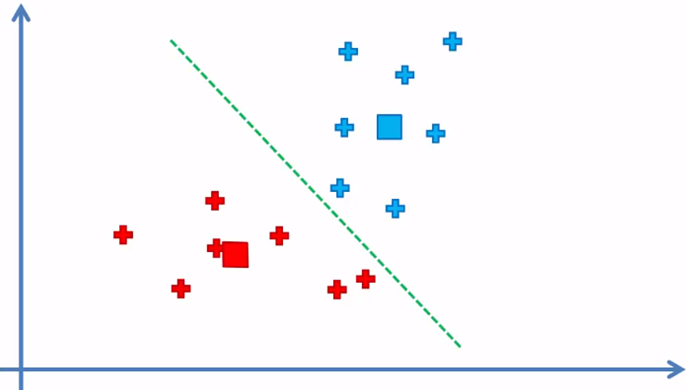
Cuando ya no hay elementos que cambiaron de cluster, el modelo ha terminado y tenemos los dos clusters con sus respectivos elementos de la muestra de datos.

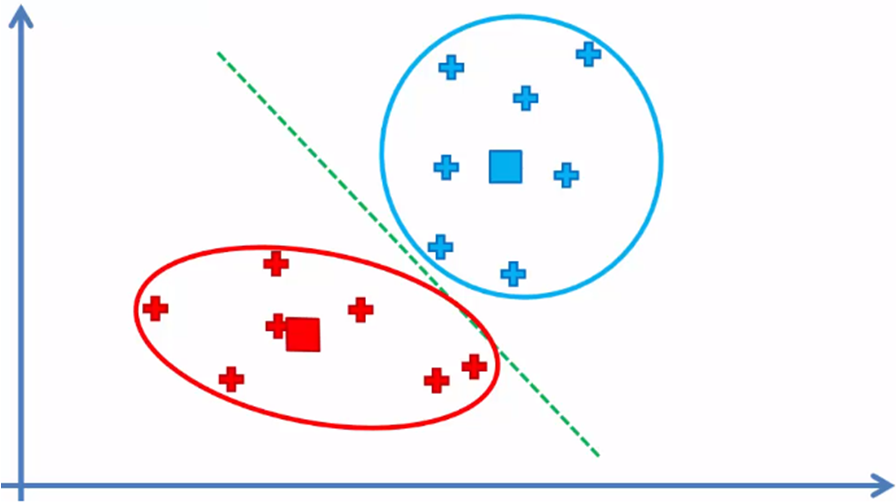
Dado que los centroides no son parte del conjunto de datos, estos no se toman en cuenta.

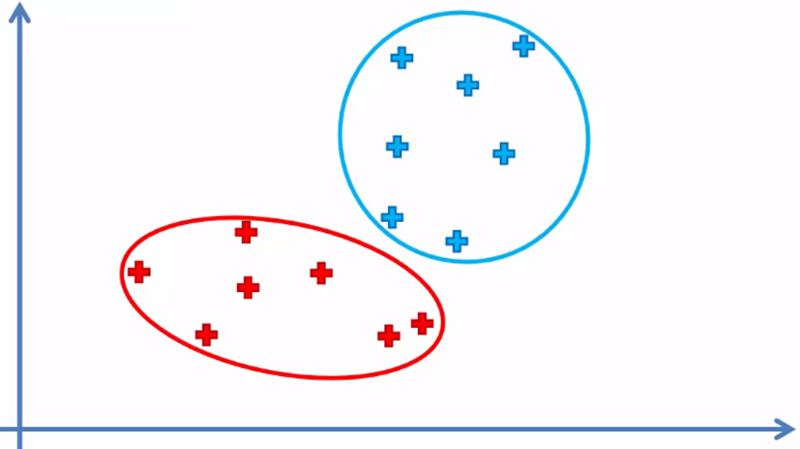
Como se puede intuir, la posición inicial de los centroides puede influir en la agrupación final de todos elementos y esto generar más de una solución para la misma cantidad de clusters

Por ejemplo, para un mismo conjunto de datos, podríamos tener dos o más agrupar los elementos de datos, dependiendo de la posición inicial de los centroides. En la siguiente imagen comparativa, tenemos k = 3 y dos opciones finales para el mismo conjunto de datos:

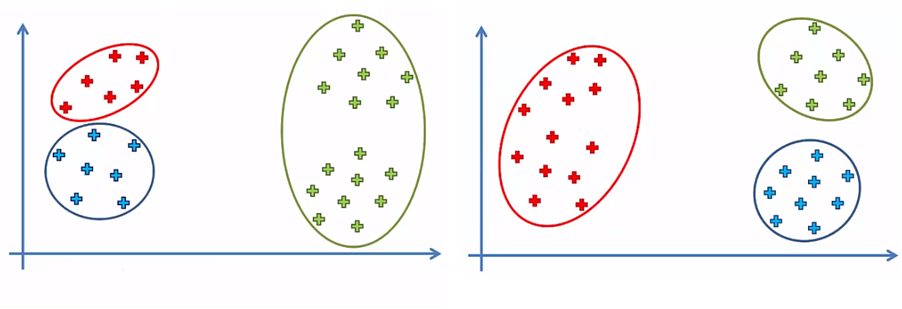
Esta ambigüedad se resuelve con una pequeña modificación al algoritmo k-Means que lo convierte en k-Means++

Selección del número correcto de clusters k

Para determinar el número óptimo de clusters que se pueden tener en una muestra de datos, existen varios métodos prácticos tanto formales como gráficos que se pueden utilizar, pero una de las técnicas más comunes y robustas, es el método del codo.

El método del codo se basa en la suma de los cuadrados de las distancias de cada elemento de datos con su centroide correspondiente y se denota de la siguiente manera:

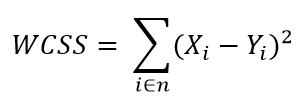
Donde WCSS es la suma de los cuadrados de las distancias y se refiere a Within-Cluster-Sum-of-Squares, Y_i es el centroide del elemento o dato X_i y n el total de datos en la muestra.

El proceso se lleva a cabo iniciando con un solo cluster para todos los elementos de la muestra y se obtiene la suma de todas las distancia de cada elemento con el centroide, posteriormente se crean dos centroides y se suman los elementos más cercanos a cada uno de los centroides para sumar las distancias de cada elemento con su centroide correspondiente. El proceso se repite para 3, 4, 5 … n centroides. Cuando el número de centroides es igual a la cantidad de datos de la muestra (n), las distancias son cero, dado que cada elemento es un centroide.

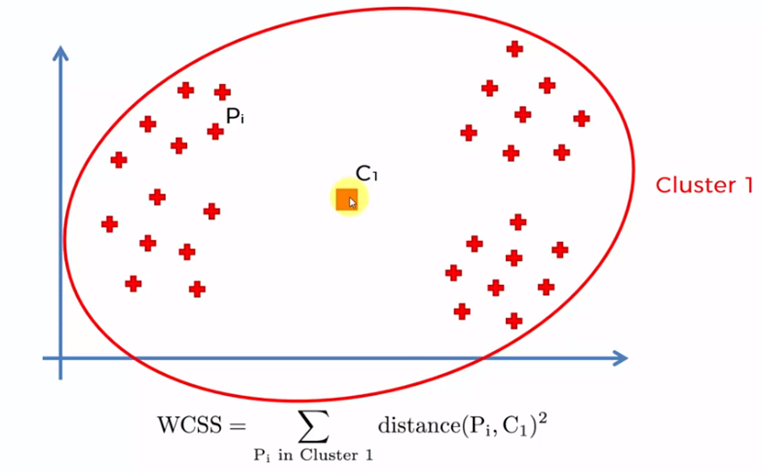
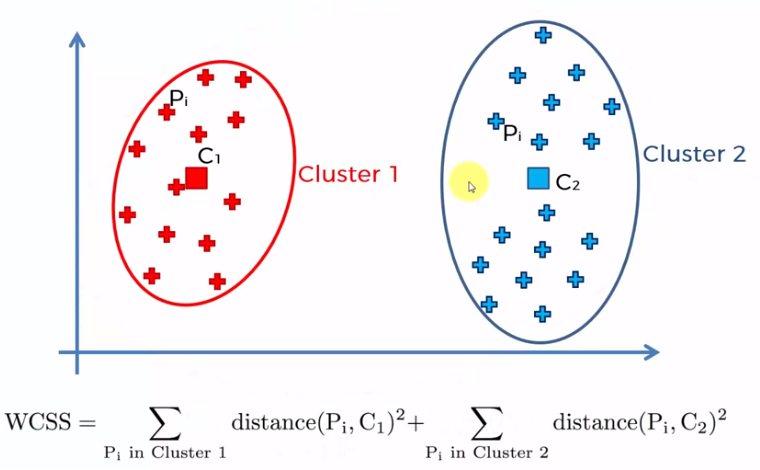
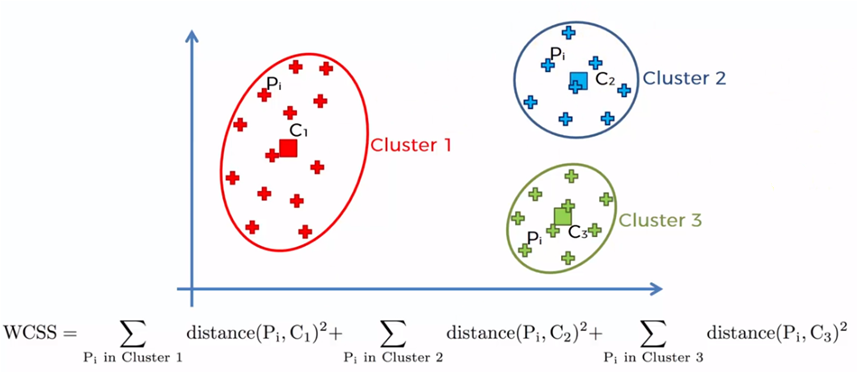
Cada uno de estos valores de WCSS para cada caso, es decir, 1 centroide, 2 centroides, etc. se grafica y obtenemos una gráfica similar a la siguiente:

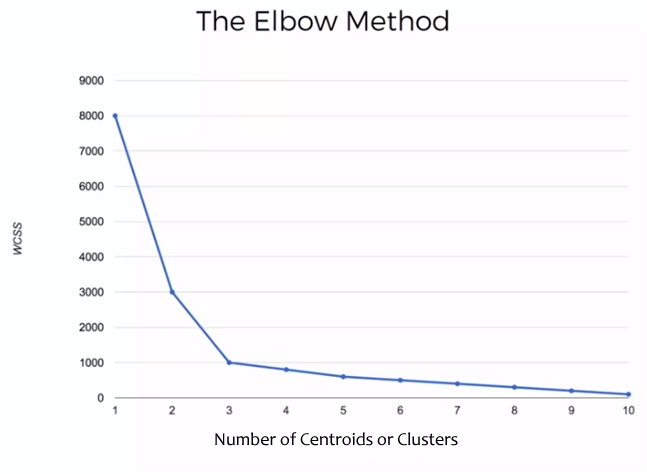
En este ejemplo se realizó el cálculo de la suma de las distancias para 1 a 10 clusters y/o centroides.

El la gráfica se observa que la suma de las distancias disminuye conforme aumenta el número de clusters y esa disminución se va atenuando conforme aumentan los número de clusters. El punto en donde se hace un codo y el cambio en el valor de la suma de las distancias se reduce significativamente, es el valor que nos indica el número óptimo de clusters que deberá tener la muestra. En este caso el punto óptimo es 3

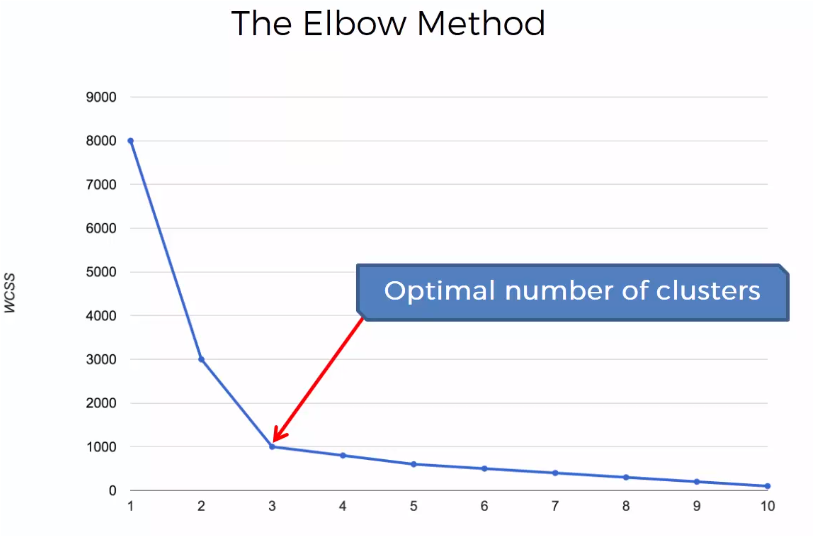
Para generar la gráfica, no es necesario genera los n centroides, cuando n es el número de muestras en el conjunto de datos, un valor estimado que permita visualizar la gráfica con el codo será suficiente para determinar ese número óptimo para los clusters que generará el método k-Means.

Implementación de k-Means con Python

El dataset utilizado en el ejemplo lo puedes descargar de este enlace: dataset

Para este ejemplo con python, utilizaremos una muestra de 200 datos de una tienda que ha calificado a sus clientes con una puntuación que va de 1 a 100 de acuerdo a su frecuencia de compra y otras condiciones que ha utilizado dicha tienda para calificar a sus clientes con esa puntuación. En el conjunto de datos tenemos información sobre el género, la edad y el ingreso anual en miles del cliente. Sin embargo, para poder graficar los resultados sólo utilizaremos el ingreso anual y la puntuación para generar los grupos de clientes que existen en esta muestra y analizar dicho resultado.

# K-Means Clustering

# Importacion de librerias
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Carga del conjunto de datos
dataset = pd.read_csv('Clientes_Tienda.csv')
X = dataset.iloc[:, [3, 4]].values

Importamos las librerías y cargamos el conjunto de datos, indicando que la variable que se analizará es una matriz con las columnas 3 y 4 de conjunto de datos, las cuales corresponden al ingreso anual en miles y la puntuación del cliente.

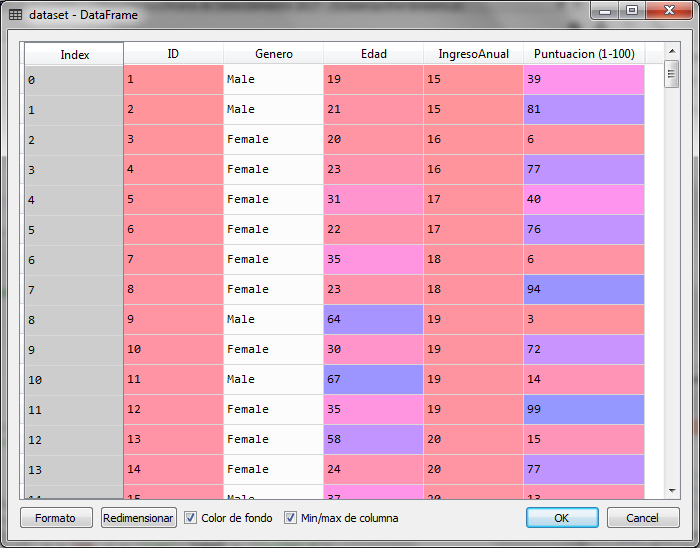
La matriz de X es la siguiente:

Nuestro siguiente paso será crear la gráfica para el método del codo y determinar el número óptimo de clusters que existen en la muestra de acuerdo al ingreso y la puntuación que le asigno la tienda a cada uno de los clientes.

# Metodo del Codo para encontrar el numero optimo de clusters

from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)

# Grafica de la suma de las distancias
plt.plot(range(1, 11), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()

En el bloque anterior, generamos los clusters para valores de 1 a 10 (en el rango de 1 a 11) y obtenemos para cada uno de ellos, la suma de las distancias con el tributo inertia_ del objeto kmeans. La gráfica obtenida es la siguiente:

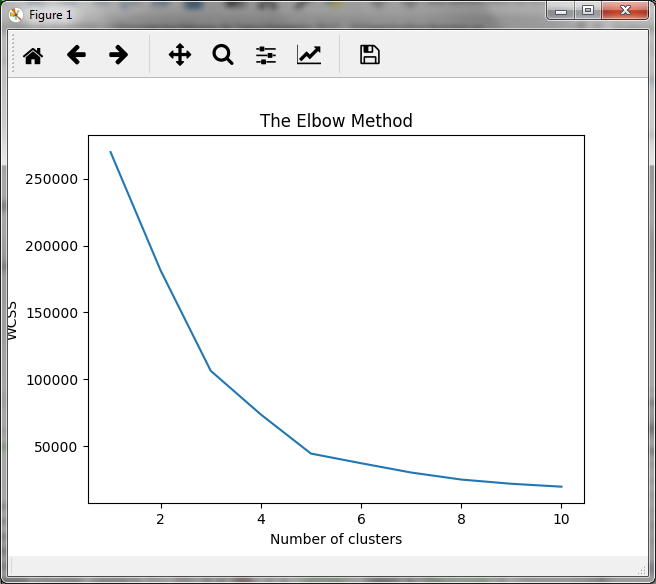
El la gráfica observamos que la disminución en la suma de las distancias se atenúa cuando el número de clusters es igual a 5, por lo que, para este caso práctico, el número óptimo de clusters será de 5.

Con ello, ahora generamos el modelo para 5 clusters con el objeto kmeans

# Creando el k-Means para los 5 grupos encontrados
kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)

la variable y_kmeans guarda los grupos que corresponden a cada renglón de la muestra de datos, lo que significa que cada registro que corresponde a un cliente, esta asignado a uno de cinco grupos que van de 0 a 4

Para poder observar gráficamente la asignación de los 200 clientes a 5 grupos o clusters realizamos lo siguiente, le asignamos un color a cada grupo y marcamos los centroides en amarillo:

# Visualizacion grafica de los clusters
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 100, c = 'red', label = 'Cluster 1')
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Cluster 2')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Cluster 3')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4')
plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5')

plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 300, c = 'yellow', label = 'Centroids')

plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()

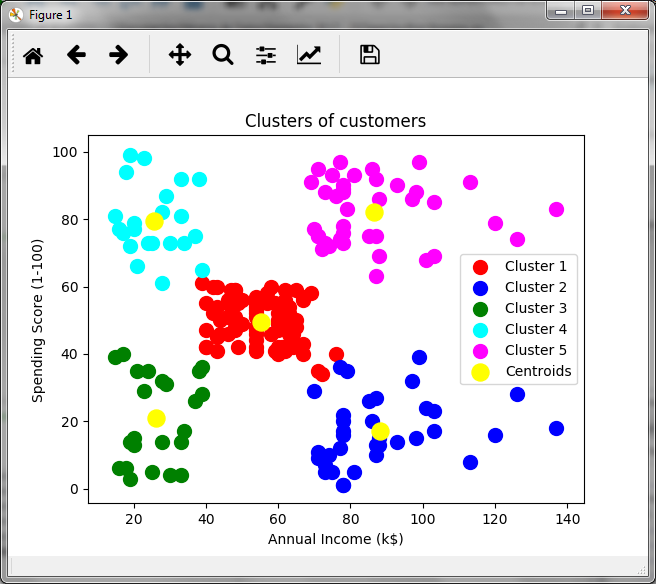
En relación al ingreso anual en miles y la puntuación generada por la tienda, observamos un grupo de clientes que podría ser de interés para la tienda. El grupo de clientes en color púrpura, lo cuales tienen ingresos altos y una puntuación alta, por lo que podrían ser un grupo objetivo para ciertas promociones. En verde tenemos a los clientes de baja puntuación y bajos ingresos, mientras que en azul, a los clientes con ingresos bajos pero con alta puntuación, lo cual podría indicar que estos clientes compran mucho a pesar de los ingresos bajos. Es decir, el análisis cluster permite hacer inferencias y tomar decisiones.

En el siguiente artículo, resolvemos el mismo caso pero con el método jerárquico