Clustering Jerárquico con Python

Como su nombre lo indica, el clustering Jerárquico construye una jerarquía de clusters para realizar el análisis y existen dos categorías para este tipo de clustering:

• Aglomerante
• Divisivo

Para representar los resultados de la jerarquía de grupos se usa el dendograma que muestra las jerarquías de acuerdo a las distancias que existen entre los elementos del conjunto de datos, las cuales se pueden representar en una matriz de distancias.

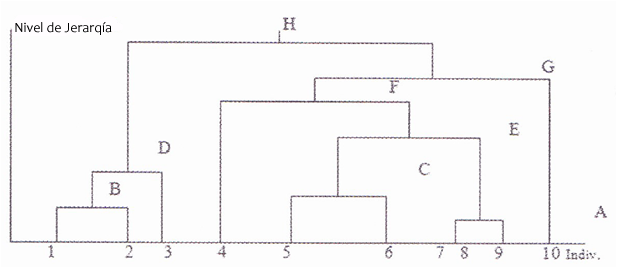
Clustering Jerárquico Aglomerante

Es una aproximación de abajo hacia arriba (bottom-up) donde se dividen los clusters en subclusters y así sucesivamente. Iniciando asignando cada muestra simple a un cluster y en cada iteración sucesiva va aglomerando (mezclando) el par de closters más cercanos satisfaciendo algún criterio de similaridad, hasta que todos los elementos pertenecen a un solo cluster. Los clusters generados en los primeros pasos son anidados con los clusters generados en los siguientes pasos.

El proceso de cluster aglomerante es el siguiente:

• Primero asigna cada elemento a un cluster
• Después encuentra la matriz de distancias
• Encuentra 2 clusters que tengan la distancia más corta y los mezcla
• Continua este proceso hasta que se forma un solo cluster grande

El siguiente diagrama muestra el proceso aglomerante

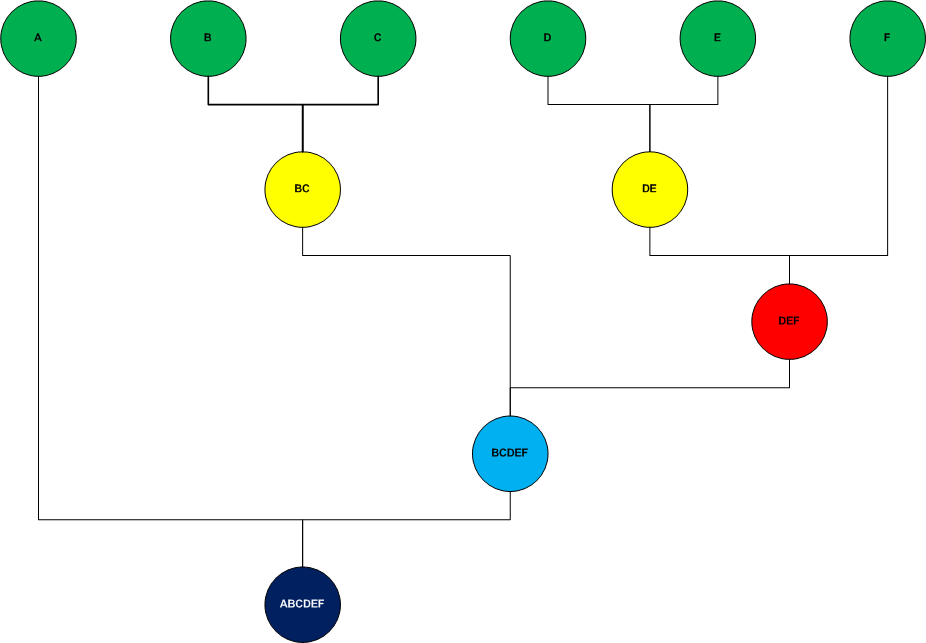
Clustering Jerárquico Divisivo

Este tipo de clustering se lleva a cabo con un enfoque de arriba hacia abajo (top-down), Se inicia con todos los elementos asignado a un solo cluster y sigue el algoritmo hasta que cada elemento es un cluster individual.

A diferencia del enfoque de abajo hacia arriba donde las decisiones para generar los clusters se basan en lo patrones locales sin tomar en cuenta la distribución global, el enfoque de arriba hacia abajo se beneficia de la información completa sobre la distribución global al ir haciendo las particiones.

El siguiente diagrama muestra el proceso divisivo

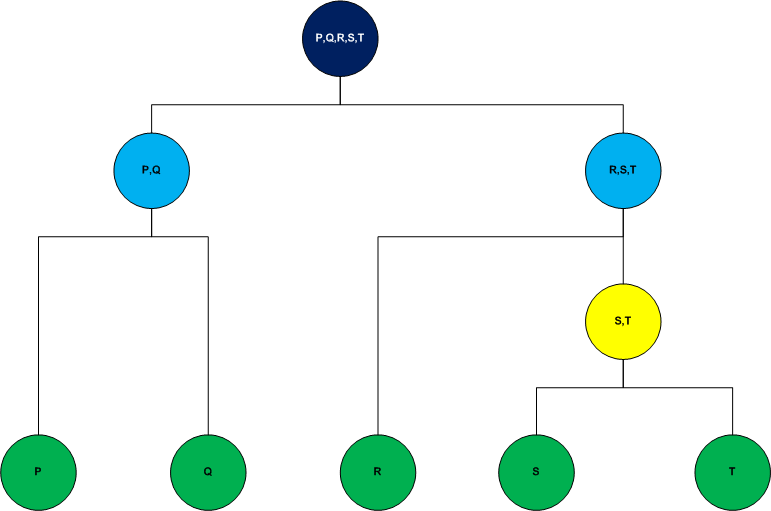
Para ambos casos, la medida de distancia que se utiliza para generar los clusters es comúnmente la distancia euclidiana. Se puede seleccionar otro método de acuerdo la relevancia del problema, pero, generalmente la distancia euclidiana es la más eficiente si no existen restricciones en el modelo.

También puedes ver el tema en video. Ingresa también a Youtube y suscribete al canal

Clustering Jerárquico en Video

Implementación del enfoque Aglomerante con Python

Como se mencionó anteriormente, el enfoque aglomerante es un enfoque de abajo hacia arriba (bottom-up) en donde inicialmente cada elemento es considerado un cluster, posteriormente se toman los dos puntos más cercanos y se forma un cluster de dos elementos, a partir de ahí se localizan los clusters más cercanos para formar un nuevo cluster y así sucesivamente, hasta que todos los elementos pertenece a un solo cluster. Con ello creamos el dendograma para decidir cuantos cluster tendrá la muestra de datos.

Para este ejemplo con python, utilizaremos una muestra de 200 datos de una tienda que ha calificado a sus clientes con una puntuación que va de 1 a 100 de acuerdo a su frecuencia de compra y otras condiciones que ha utilizado dicha tienda para calificar a sus clientes con esa puntuación. En el conjunto de datos tenemos información sobre el género, la edad y el ingreso anual en miles del cliente. Sin embargo, para poder graficar los resultados sólo utilizaremos el ingreso anual y la puntuación para generar los grupos de clientes que existen en esta muestra y analizar dicho resultado con el enfoque aglomerante.

Puedes descargar el archivo de datos para el ejercicio siguiente en este enlace: Clientes_Tienda.csv

# Clustering Jerárquico

# Importacion de librerias
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Carga del conjunto de datos
dataset = pd.read_csv('Clientes_Tienda.csv')
X = dataset.iloc[:, [3, 4]].values

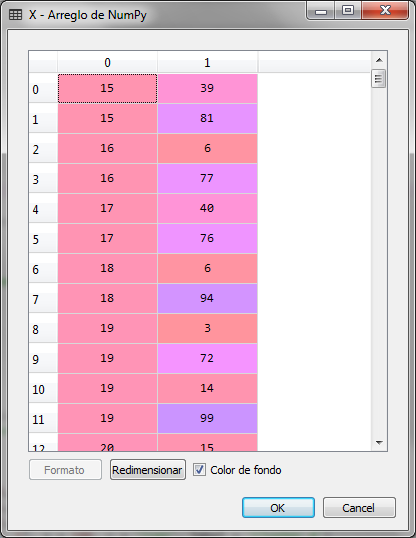
Importamos las librerías y cargamos el conjunto de datos, indicando que la variable que se analizará es una matriz con las columnas 3 y 4 de conjunto de datos, las cuales corresponden al ingreso anual en miles y la puntuación del cliente.

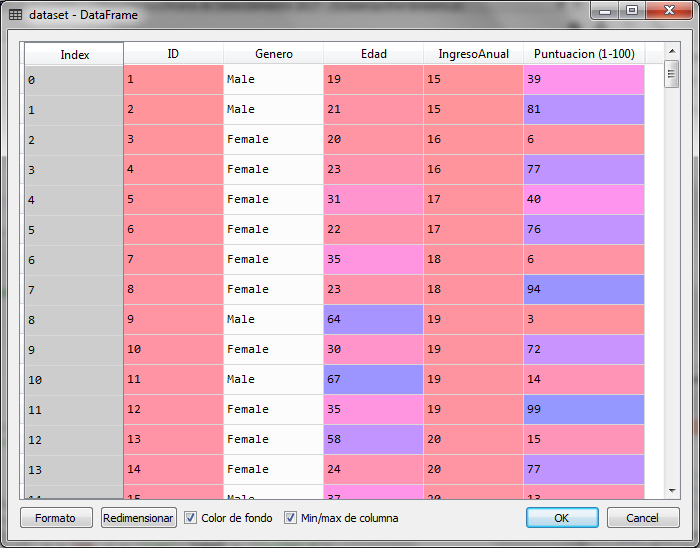
La matriz X es la siguiente:

Para crear el dendograma utilizamos la clase sch del paquete scipy.hierarchy

# Creamos el dendograma para encontrar el número óptimo de clusters

import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method = 'ward'))

plt.title('Dendograma')
plt.xlabel('Clientes')
plt.ylabel('Distancias Euclidianas')
plt.show()

El ejecutar el bloque anterior obtenemos el diagrama del dendograma

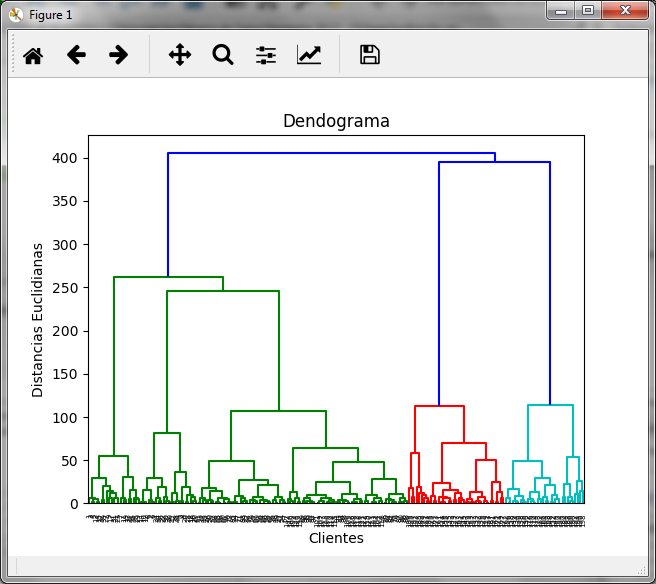
En el podemos observar que la distancia máxima la marca la línea azul oscuro que une los clusters rojo y azul claro, por lo que si realizamos el corte en esa zona obtenemos:

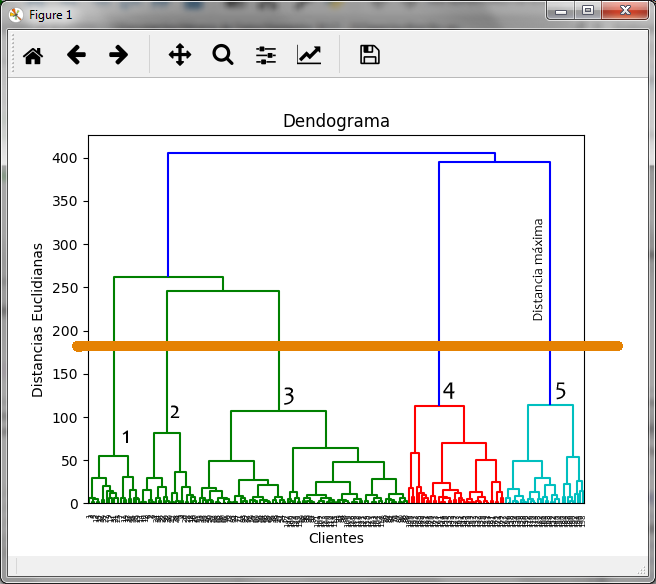
Al marcar con la línea color naranja el dendograma donde observamos la distancia máxima, nos genera 5 clusters que hemos marcado con números.

Con ello en mente, generamos los grupos con el método aglomerante utilizando la clase AgglomerativeClustering del paquete sklearn.cluster

# Ajustando Clustering Jerárquico al conjunto de datos
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters = 5, 
                    affinity = 'euclidean', 
                    linkage = 'ward')

y_hc = hc.fit_predict(X)

En la variable y_hc se guardan los grupos asignados a cada cliente o renglón del conjunto de datos. En ese vector podemos observar los 5 grupos que van de 0 a 4

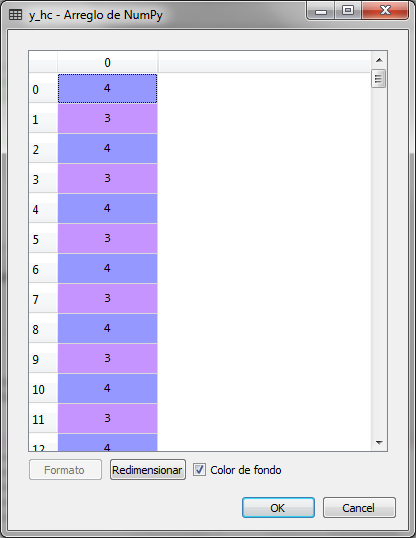
Para poder observar gráficamente la asignación de los 200 clientes a 5 grupos o clusters realizamos lo siguiente:

# Visualising the clusters
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1], s = 100, c = 'red', label = 'Cluster 1')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1], s = 100, c = 'blue', label = 'Cluster 2')
plt.scatter(X[y_hc == 2, 0], X[y_hc == 2, 1], s = 100, c = 'green', label = 'Cluster 3')
plt.scatter(X[y_hc == 3, 0], X[y_hc == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4')
plt.scatter(X[y_hc == 4, 0], X[y_hc == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()

La gráfica obtenida es la siguiente:

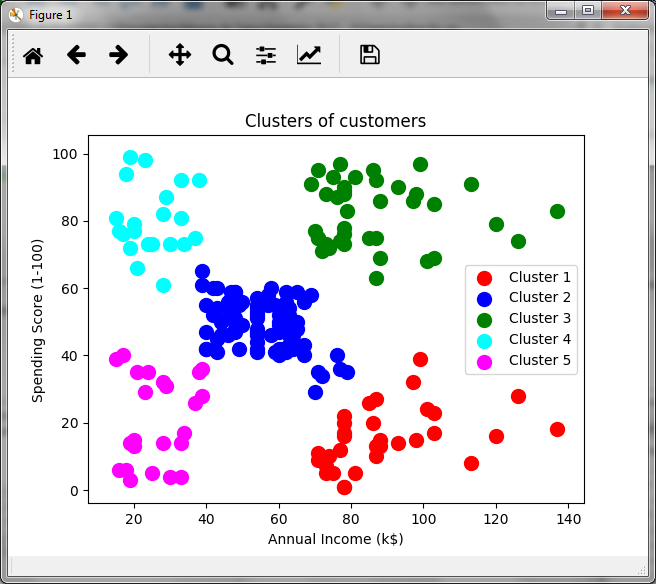
En relación al ingreso anual en miles y la puntuación generada por la tienda, observamos un grupo de clientes que podría ser de interés para la tienda. El grupo de clientes en color verde, lo cuales tienen ingresos altos y una puntuación alta, por lo que podrían ser un grupo objetivo para ciertas promociones. En purpura tenemos a los clientes de baja puntuación y bajos ingresos, mientras que en azul claro, a los clientes con ingresos bajos pero con alta puntuación, lo cual podría indicar que estos clientes compran mucho a pesar de los ingresos bajos. Es decir, el análisis cluster permite hacer inferencias y tomar decisiones de negocios.

En el artículo anterior k-Means Clustering resolvemos el mismo caso pero con el método k-Means y obtenemos los mismos resultados.

Una de las desventajas del método jerárquico es que no es muy recomendable para problemas con grandes cantidades de datos, debido a que se generaría un dendograma difícil de manipular para seleccionar el número óptimo de clusters.