Clustering Analysis
El análisis clustering o de conglomerados es una técnica de clasificación y segmentación que pertenece a la categoría de aprendizaje no supervisado.
Identifica grupos de sujetos lo más heterogéneos posible entre sí y lo más homogéneo posible dentro de cada grupo.
El análisis establece los grupos basándose en la similitud que presentan las entidades respecto a una serie de características que se especificaron previamente. Por lo que es el análisis y no el analista quien extrae los grupos de sujetos y sus características definitorias.
El clustering es un algoritmo de agrupamiento cuyo objetivo es realizar agrupaciones de datos de acuerdo a un criterio, que por lo general este criterio es la distancia o similitud.
Esta similitud se define en términos de una función de distancia, como la distancia euclidiana. Aunque existen otras funciones de distancia más robustas o que permiten incluir variables discretas, la euclidiana es una de las más aceptadas. Adicionalmente, la medida más empleada para validar la similitud entre los casos es la matriz de correlación entre los nxn casos.
Su finalidad es revelar concentraciones en los datos o casos para su agrupamiento eficiente en clusters o conglomerados según su homogeneidad y se pueden utilizar tanto variables cualitativas como variables cuantitativas, dado que los grupos se basan en la proximidad o lejanía de unos con otros.
En este sentido, los grupos no se conocen de antemano, pero quizás se sugieren por la esencia de los datos. En otros análisis, como el caso del análisis discriminante, los grupos se definen previamente (ad hoc), en el clustering no se especifican previamente (post hoc).
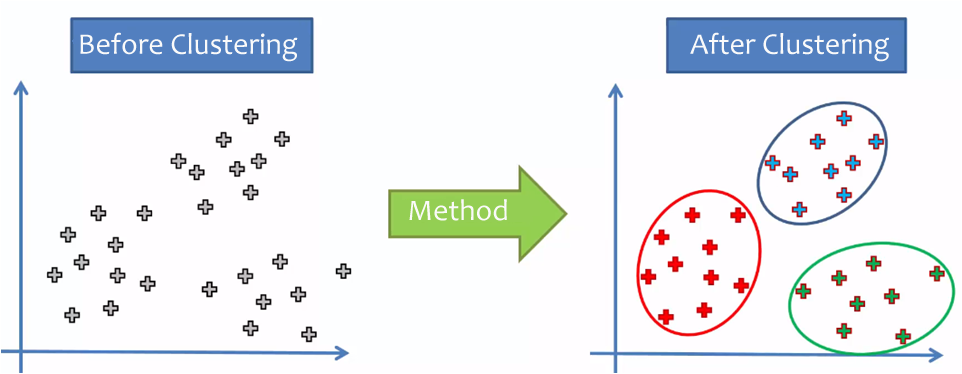
Casos y Variables
Si las variables de aglomeración están en escalas distintas, será necesario estandarizar o trabajar con desviaciones respecto a la media. Para el caso de los valores desaparecidos o faltantes, se sugiere eliminar los casos dado que los métodos jerárquicos no tienen solución con valores perdidos.
En cuanto a los valores atípicos, estos deforman las distancias y producen clusters unitarios. Por lo que deben ser eliminados de la muestra.
Si existen variables correlacionadas será necesario un análisis de multicolinealidad previo o un análisis factorial.
Por otro lado, la solución del análisis de cluster no tiene por que ser única, sin embargo, no deben existir soluciones contradictorias al usar distintos métodos de agrupamiento.
Adicionalmente, el número de observaciones en cada cluster debe ser relevante y estos deben tener sentido conceptual y no variar mucho al variar la muestra o el método de aglomeración.
Los grupos finales serán tan distintos como permitan los datos y con ellos se podrán realizar otros análisis ya sea descriptivos, discriminante, regresión logistica, diferencia u otros.
Métodos de clustering
En cuanto a los métodos de agrupamiento, existen dos categorías generales:
- Métodos jerárquicos, que pueden ser aglomerativos o divisivos
- Métodos no jerárquicos, en los que el número de clusters o grupos se determina de antemano con una técnica previa y los casos se van asignando a los grupos en función de su cercanía.
Los métodos más utilizados son a la vez secuenciales, aglomerativos, jerárquicos y exclusivos. En todos ellos se siguen dos pasos fundamentales en el proceso de elaboración de los conglomerados:
- El primero es que los coeficientes de similitud o disimilitud entre los nuevos conglomerados establecidos y los candidatos potenciales a ser admitidos se recalculan en cada etapa.
- y el segundo, es el criterio de admisión de nuevos miembros a un conglomerado ya establecido.
Métodos Jerárquicos
En este tipo de clustering los dos clusters más similares se van combinando hasta que todos los casos similares estén en el mismo cluster.
Existen dos enfoques principales para los cluster jerárquicos:
- Aglomerativo o de abajo hacia ariba (bottom-up) donde tomamos cada unidad como un cluster individual y se van combinando para formar clusters más grandes
- Divisible o de arriba hacia abajo (top-down) donde se inicia con un conjunto completo y se van dividiendo sucesivamente en clusters más pequeños.
Métodos no Jerárquicos
En los métodos de agrupamiento no jerárquico se consideran todos los clusters a la vez, dado que se requiere especificar en número de grupos que se van a generar. El método no jerárquico más utilizado es el k-Means, el cual es un modelo de centroides.
k-Means es un método rápido, robusto y fácil de entender, lo que hace relativamente eficiente si los datos están conformados por unidades distintas y bien separadas. Su principal desventaja es que se requiere el valor de k antes de iniciar el algoritmo. Por otro lado, si los datos se traslapan será más difícil formar los clusters.
Otra desventaja es que el método depende de la media y si los datos con categóricos, no existe tal media y por lo tanto no es posible usar el método k-Means.
Los métodos no jerárquicos son más recomendados para grandes cantidades de datos y son también útiles para la detección de casos atípicos.
En los siguientes artículos se describen los métodos de agrupamiento o clustering más comúnmente utilizados: k-Means y Jerárquico y se presentan ejemplos de implementación con Python:
La siguiente tabla presenta una comparativa de ambos métodos
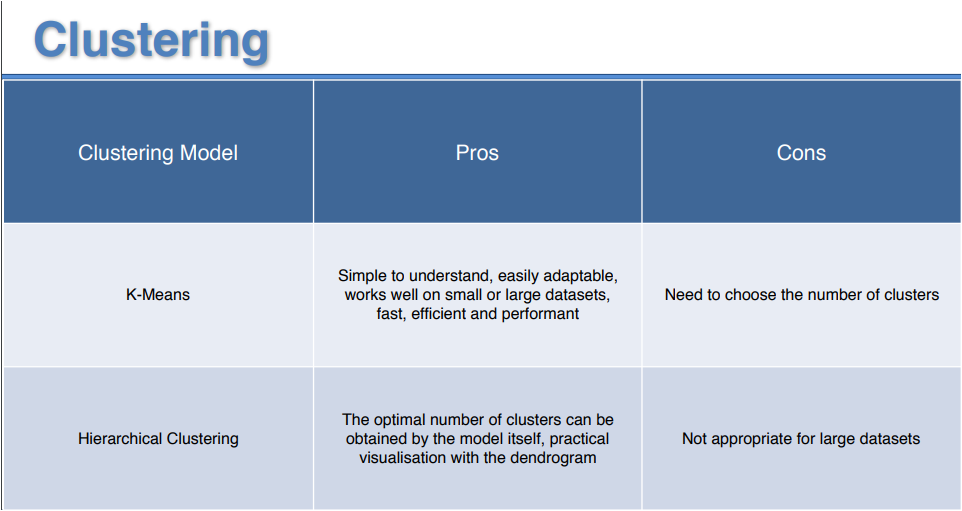

[…] se describió en el artículo anterior: Cluster Analysis, el método k-Medias es un método no jerárquico basado en centroides, robusto y fácil de […]