Clasificador Naive Bayes con Python

Tanto en probabilidad como en minería de datos, un clasificador ingenuo Bayesiano (clasificador naive bayes) es un método probabilístico que tiene sus bases en el teorema de Bayes y recibe el apelativo de ingenuo dadas algunas simplificaciones adicionales que determinan la hipótesis de independencia de las variables predictoras.

Si quieres verlo en video:

El argumento de Bayes no es que el mundo sea intrínsecamente probabilístico o incierto, sino que aprendemos sobre el mundo a través de la aproximación, acercándonos cada vez más a la verdad, a medida que recogemos más evidencias.

En términos sencillos, el clasificador ingenuo de Bayes asume que la presencia o ausencia de una característica particular no está relacionada con la presencia o ausencia de cualquier otra característica. Por ejemplo, una fruta puede ser considerada como una manzana si es roja, redonda y de alrededor de 7 cm de diámetro.

Un clasificador ingenuo de Bayes considera que cada una de estas características contribuye de manera independiente a la probabilidad de que esta fruta sea una manzana, independientemente de la presencia o ausencia de las otras características.

En muchas aplicaciones prácticas, la estimación de parámetros para los modelos de Bayes utilizan el método de máxima verosimilitud, es decir, se puede trabajar con el modelo ingenuo de Bayes sin aceptar la probabilidad bayesiana o cualquiera de los métodos bayesianos.

Una ventaja del clasificador ingenuo de Bayes es que solo se requiere una pequeña cantidad de datos de entrenamiento para estimar los parámetros necesarios para la clasificación (las medidas y las varianzas de las variables).

Solo es necesario determinar las varianzas de las variables de cada clase y no toda la matriz de covarianza. Para otros modelos de probabilidad, los clasificadores ingenuos de Bayes  se pueden entrenar en entornos de aprendizaje supervisado. 

Teorema de Bayes

El teorema de bayes esta expresado por la siguiente ecuación:

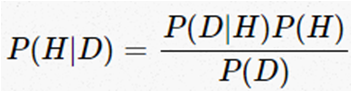
P(H) es la probabilidad a priori, la forma de introducir conocimiento previo sobre los valores que puede tomar la hipótesis.

P(D|H) es el likelihood de una hipótesis H dados los datos D,  es decir, la probabilidad de obtener D dado que H es verdadera.

P(D) es el likelihood marginal o evidencia, es la probabilidad de observar los datos D promediado sobre todas las posibles hipótesis H.

P(H|D) es el a posteriori, la distribución de probabilidad final para la hipótesis. Es la consecuencia lógica de haber usado un conjunto de datos, un likelihood y un a priori.

Sobre una variable dependiente H, con un pequeño número de clases, la variable esta condicionada por varias variables independientes D = {d1, d2, …, dn} las cuales, dado el supuesto de independencia condicional de bayes, se asume que cada di es independiente de cualquier otro dj para i diferente de j y la podemos expresar en términos simples de la siguiente forma:

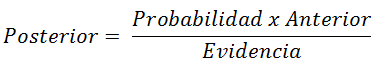
La formula nos indica la probabilidad de que una hipótesis H sea verdadera si algún evento D ha sucedido. Esto es importante dado que, normalmente obtenemos la probabilidad de los efectos dadas las causas, pero el teorema de bayes nos indica la probabilidad de las causas dados los efectos.

Por ejemplo, podemos saber cual es el porcentaje de pacientes con gripe que tienen fiebre, pero lo que realmente queremos saber es la probabilidad de que un paciente con fiebre tenga gripe.

Ejemplo

Tenemos dos máquinas (m1 y m2) que fabrican la misma herramienta

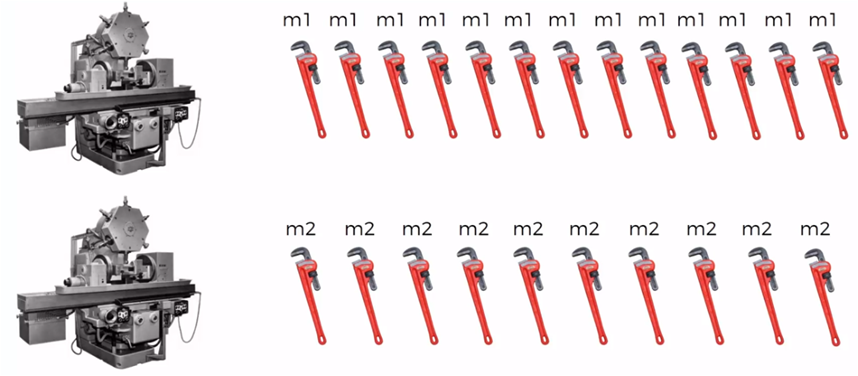
De todas las herramientas que fabrica cada una de las máquinas, algunas se producen con defectos.

Si consideramos que la máquina 1 produce 30 llaves por hora y la máquina 2 produce 20 llaves por hora, de todas las partes producidas se observa que el 1% están defectuosas y de todas las llaves defectuosas el 50% provienen de la máquina 1 y el 50% de la máquina 2.

¿Cuál es la probabilidad de que una pieza defectuosa haya sido producida por la máquina 2?

Si M1: 30 llaves/hora, M2: 20 llaves/hora
de las defectuosas 50%  son de M1 y 50% de M2

P(M1) = 30/50 = 0.6
P(M2) = 20/50 = 0.4
P(Defecto) = 1%
P(M1 | Defecto) = 50%
P(M2 | Defecto) = 50%

Lo que deseamos conocer es entonces:
P(Defecto | M2) = ?

Aplicando el Teorema de Bayes

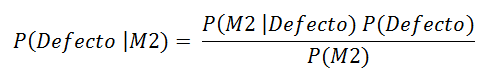
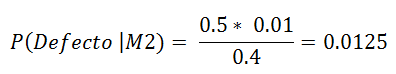
La probabilidad de que una pieza defectuosa sea de la máquina 2 es del 1.25%

En una producción de 1,000 piezas, entonces 400 provienen dela máquina 2 y si el 1% esta defectuosa habrá 10 piezas defectuosas. de esas 10 piezas el 50% son la máquina 2, es decir 5 piezas, podemos comprobar que el porcentaje de piezas defectuosas de la máquina 2 es 5/400 = 0.0125

Algoritmo del Clasificador Naive Bayes

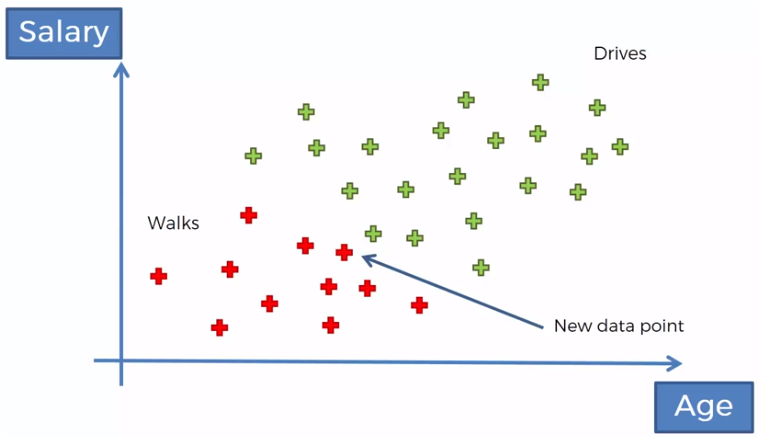
Tenemos un conjunto de datos de personas que camina o conducen hacia su trabajo, en relación a su edad y a su salario, por ejemplo. 

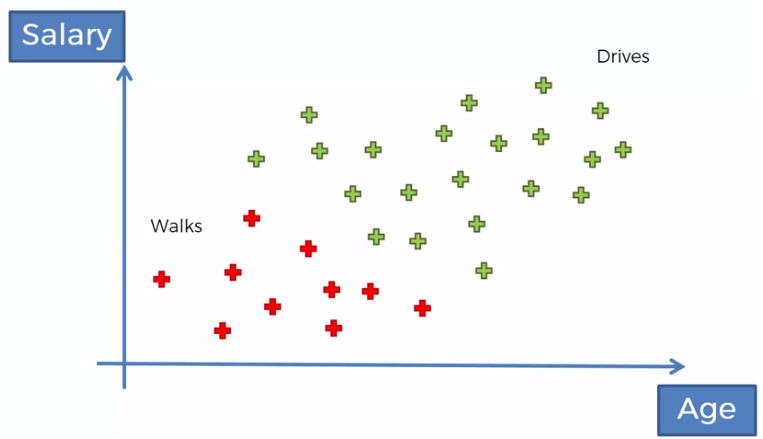
Si ahora tenemos la edad y el salario de una nueva persona, queremos clasificarla, de acuerdo a esos datos, si es de las personas que caminan o de las que conducen.

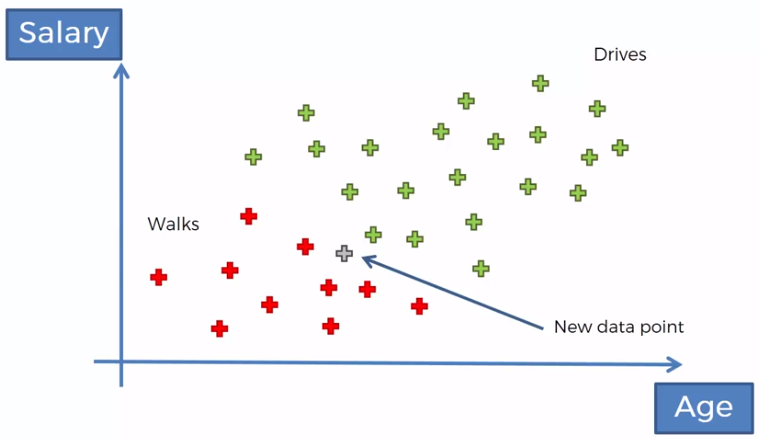
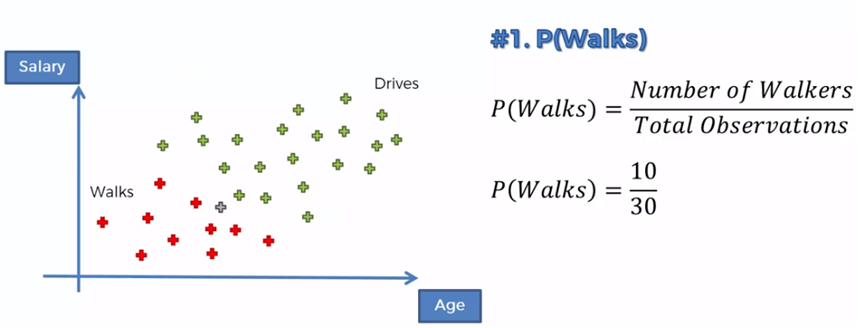
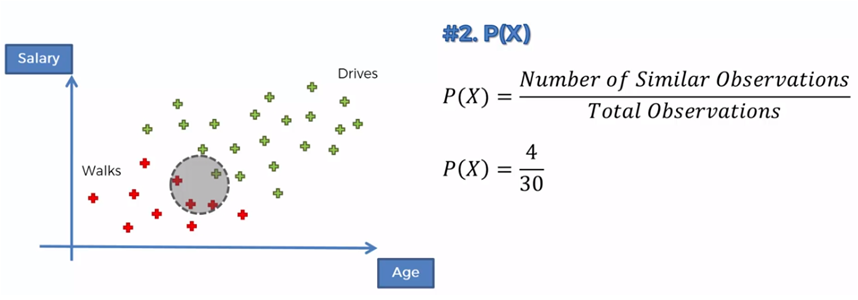
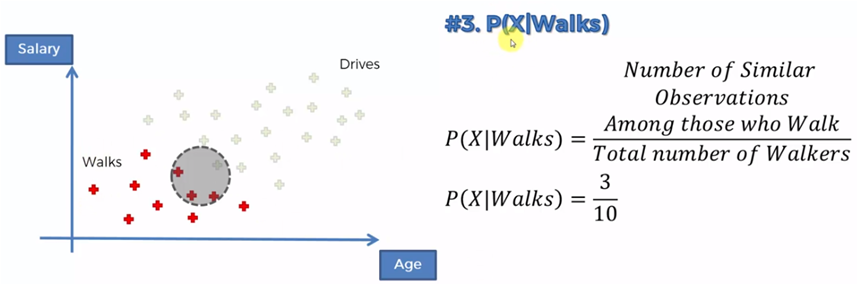
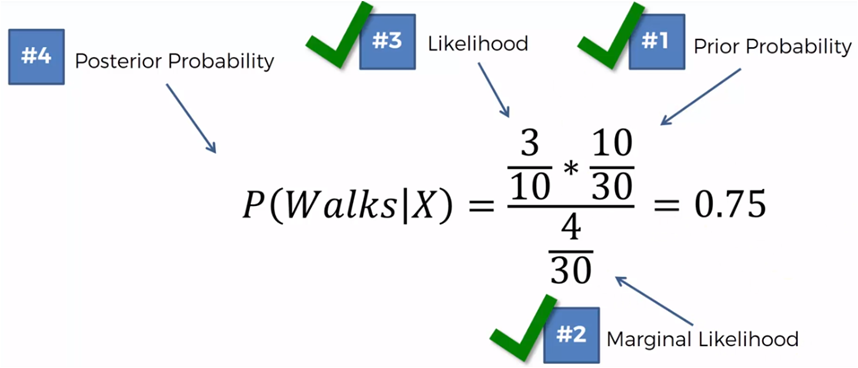
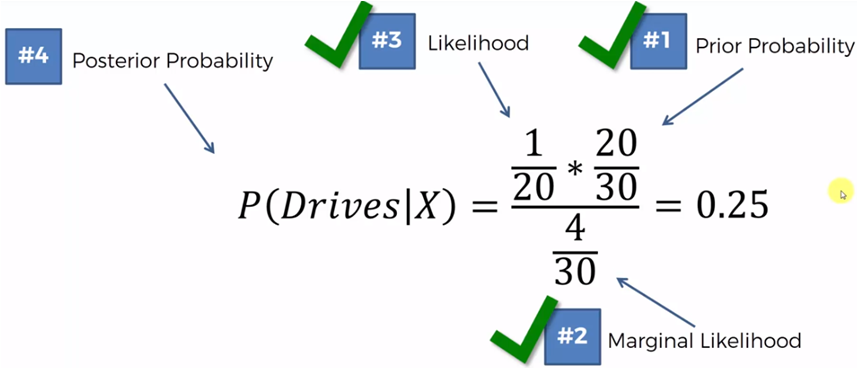
Si ahora comparamos los que caminan contra los que conducen tenemos que:

P(Camina|X) > P(Conduce |X)
0.75 > 0.25

Entonces, este nuevo punto que representa la edad y el salario de una persona nueva, será clasificado en el grupo de los que caminan.

Naive Bayes con Python

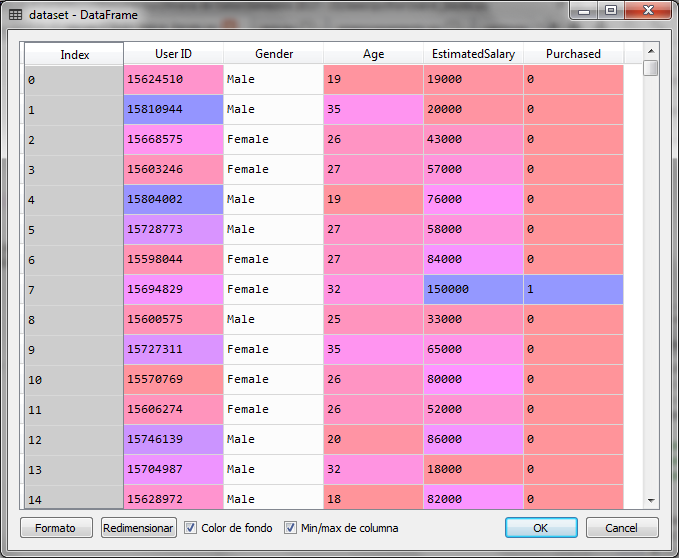
Para el ejercicio con python utilizaremos un conjunto de datos con información de clientes que compraron o no compraron en una tienda en relación a su edad y su salario principalmente.

Conclusiones

Para ahondar más sobre el tema e iniciarte con python, esta guía en video es muy buena y te permite ir de lo básico a lo intermedio: Guía en Video

Este otro más avanzado incluye análisis con pandas y otras librerías de uso frecuente: Lecciones en vivo

Adicionalmente, los fundamentos del análisis de datos con python los puedes encontrar en este video de entrenamiento.

Puedes también tomar el entrenamiento en ciencia de datos y pagar cuando hayas conseguido el trabajo como científico de datos, esta es una oferta excelente: Formación en ciencia de datos

Finalmente, la certificación AWS Asociado o AWS Profesional están muy accesibles y son herramientas indispensables en el tema.

Un webinar bastante interesante sobre Azure es el siguiente: Webinar Azure

Data analytics with Spark using Python