Análisis del Componente Principal

El PCA es una herramienta para reducir la dimensionalidad en los datos que puede ser utilizado para convertir un conjunto bastante grande de variables en un conjunto más pequeño que contenga la mayor cantidad de información contenida en el conjunto grande.

Si quieres verlo en video:

En este sentido, el PCA es un procedimiento matemático que transforma un conjunto de variables correlacionadas en un conjunto (más pequeño) de variables no correlacionadas llamadas componentes principales.

El primer componente principal representa la mayor cantidad posible de variabilidad en los datos y cada componente subsiguiente explica la mayor parte de la variabilidad restante, es decir, que el conjunto de datos de menor dimensión deberá preservar la varianza de los datos originales.

Por ejemplo, un conjunto de datos de dos dimensiones se puede reducir proyectando los puntos sobre una línea, entonces, cada instancia en el conjunto de datos puede ser representada por un solo valor en lugar de una par de valores. Un conjunto de datos de tres dimensiones se puede reducir a dos dimensiones proyectando las variables en un plano.

En general, un conjunto de n dimensiones se puede reducir proyectando el conjunto de datos en un subespacio de k dimensiones, donde k es menor a n.

De manera más formal, PCA puede ser utilizado para encontrar un conjunto de vectores que abarca un subespacio, el cual minimiza la suma del error cuadrático de los datos proyectados. La proyección retendrá la mayor proporción de la varianza de los datos originales.

PCA rota el conjunto de datos para alinearlo con sus componentes principales para maximizar la varianza contenida dentro de los primeros componentes principales. Supongamos que tenemos el siguiente conjunto de datos graficados en la figura:

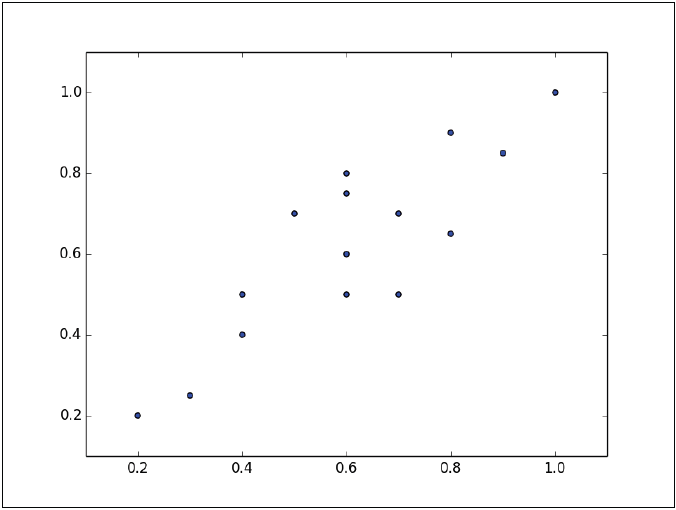
Las instancias forman una elipse aproximada que se aprecia desde el origen hacia la parte superior derecha de la gráfica. Para reducir la dimensión de este conjunto de datos, debemos proyectar los puntos en una línea. En la siguiente gráfica se muestran dos líneas en donde podrían proyectarse los datos. En cada una de ellas la varianza es distinta, por lo que la tarea es ver en cual de las dos líneas las instancias tienen la mayor variación.

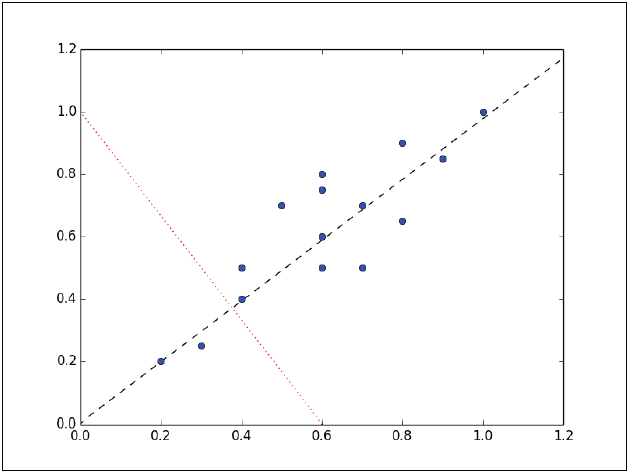
Las instancias tienen la mayor variación sobre la línea de guiones, más que sobre la línea punteada. De hecho, la línea en guiones es el primer componente principal. El segundo componente principal debe ser ortogonal al primero, esto es, que el segundo componente principal debe ser estadísticamente independiente, y al parecer será perpendicular al primero componente principal,como se muestra en la siguiente figura:

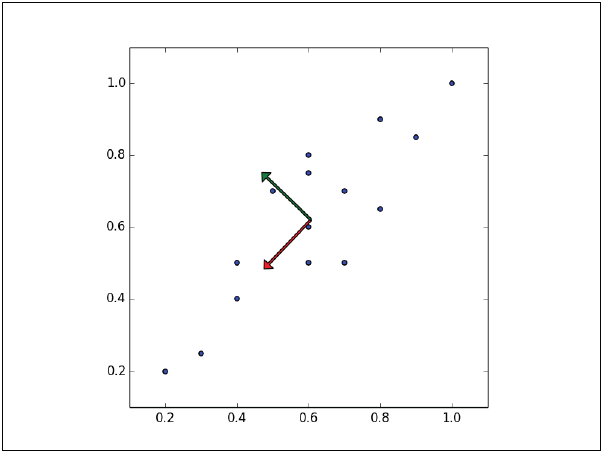
Cada componente principal subsecuente preserva la mayor cantidad de la varianza restante, la única restricción es que cada uno debe ser ortogonal al anterior.

Si ahora consideramos que los datos tienen tres variables, por lo que el conjunto de datos es tridimensional:

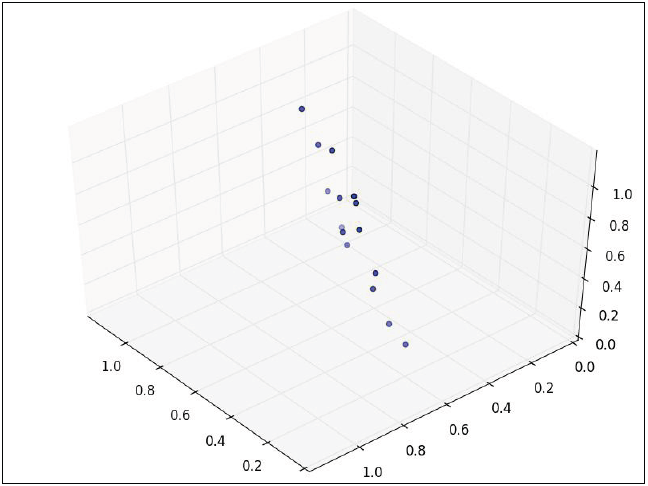
Los puntos pueden ser rotados y trasladados de tal forma que se acomoden dos dimensiones y los puntos ahora forman una elipse, la tercera dimensión casi no tendrá varianza y entonces podrá ser descartada.

El PCA es más útil cuando la varianza en el conjunto de datos esta distribuida de manera desigual a lo largo de las dimensiones. Si por el contrario, un conjunto de datos entres dimensiones forma forma una esfera convexa, el análisis PCA no podría ser tan efectivo dado que hay una varianza similar en cada dimensión, ninguna de las dimensiones podrá ser descartada sin perder información significativa.

Visualmente es más fácil identificar los componentes principales cuando el conjunto de datos esta compuesto por sólo dos o tres dimensiones. Para un conjunto de mayor dimensión los cálculos para los componentes principales se describen en la siguientes secciones.

Varianza y Covarianza

Antes de entrar de lleno con los cálculos para identificar los componentes principales, veamos algunos conceptos básicos.

Varianza

La varianza es la medida que nos indica que tan disperso o distribuido se encuentra un conjunto de valores. La varianza se calcula como el promedio del cuadrado de la diferencia de valores con respecto a la media de ese conjunto de valores:

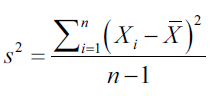
Covarianza

La covarianza es la medida de que tanto dos variables cambian juntas. Es una medida de fuerza de la correlación entre dos conjuntos de variables. Si la covarianza entre dos variables es cero, las variables no están correlacionadas. Sin embargo, el que dos variables no estén correlacionadas, no implica que sean independientes, dado que la correlación es sólo una medida de dependencia lineal y se calcula con la siguiente ecuación:

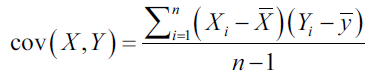
Si la covarianza no es cero, el signo indica si las variables están positiva o negativamente correlacionadas. Si dos variables están positivamente correlacionadas, significa que una incrementa su valor cuando la otra lo incrementa.

Cuando dos variables están negativamente correlacionadas significa que una variable tiene un decremento relativo a su media cuando la otra variable presenta un incremento relativo a su media.

La matriz de covarianza describe los valores de la covarianza entre cada par de valores del conjunto de datos. El elemento (i,j) indica la covarianza de la dimensión i, j de los datos. Por ejemplo, la matrizde covarianza de un conjunto de datos de tres dimensiones se vería de la siguiente forma:

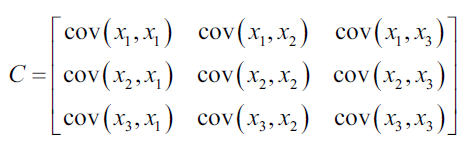
Si como ejemplo consideramos el siguiente conjunto de datos:

2	0	-1.4
2.2	0.2	-1.5
2.4	0.1	-1
1.9	0	-1.2

En la tabla anterior tenemos 3 variables como 4 casos, entonces la media de cada variable es: 2.125, 0.075 y -1.275, con ello podemos ahora calcular la covarianza de cada par de variables para generar la siguiente matriz de covarianzas.

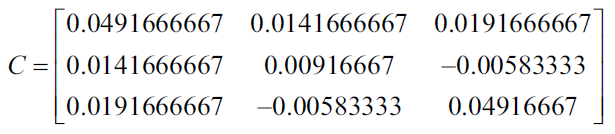
Utilizando Numpy podemos generar la matriz de covarianza de la siguiente manera:

import numpy as np
X = [[2, 0, -1.4], [2.2, 0.2, -1.5], [2.4, 0.1, -1], [1.9, 0, -1.2]]

print np.cov(np.array(X).T

out:
[[ 0.04916667 0.01416667 0.01916667]
[ 0.01416667 0.00916667 -0.00583333]
[ 0.01916667 -0.00583333 0.04916667]]

Vectores Propios y Valores Propios

Un vector se describe por su dirección y su magnitud, o longitud. Un vector propio de una matriz es un vector no cero que satisface la siguiente ecuación:

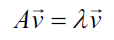
En la ecuación anterior v es el vector propio A es una matriz cuadrada y lanbda es una escalar llamado valor propio. La dirección del vector propio se mantiene igual después de ser transformado por A, sólo cambia su magnitud, dada por el valor propio, es decir que al multiplicar una matriz por uno de sus vector propios es equivalente a escalar el vector propio. 

En inglés un vector propio se conoce como eigenvector y la palabra eigen en Alemán significa pertenece a, o que es peculiar a, por lo que el vector propio de una matriz es un vector que pertenece a, y caracteriza la estructura de los datos.

Tanto los vectores propios como los valores propios sólo pueden ser derivados de matrices cuadradas y no todas las matrices cuadradas tienen vectores propios o valores propios. Si una matriz tiene vectores y valores propios, tendrá un par por cada una de sus dimensiones. Los componentes principales de una matriz  son los vectores propios de su matriz de covarianzas, ordenados por sus correspondientes valores propios.

El vector propio con el valor propio más grande es el primer componente principal, el segundo componente principal es el vector propio con el segundo valor propio más grande y así sucesivamente. 

Como ejemplo, calculemos los vectores propios y sus valores propios de la siguiente matriz cuadrada:

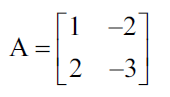
De la ecuación que mostramos previamente, recordemos que el producto de la matriz A y cualquiera de sus vectores propios debe ser igual al vector propio multiplicado por su valor propio.

Iniciemos encontrando los valores propios, los cuales se pueden encontrar con las siguientes ecuaciones características:

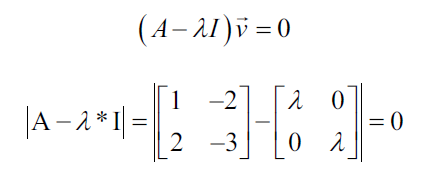
La ecuación características establece que el determinante de la matriz, esto es, la diferencia entre los datos de la matriz y el producto de la matriz identidad y un valor propio es cero:

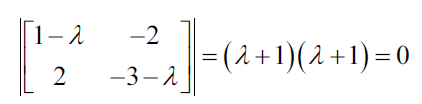
Ambos valores propios de esta matriz son iguales a -1. Por lo que ahora podemos usar los valores propios para resolver los vectores propios

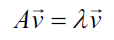
Primero, hacemos la ecuación igual a cero:

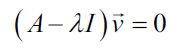
Sustituyendo los valores para A tenemos lo siguiente:

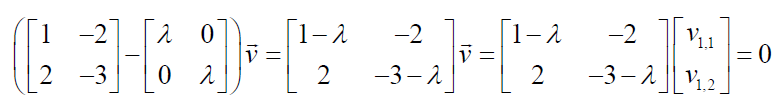
Ahora podemos sustituir el primer valor propio para resolver los vectores propios.

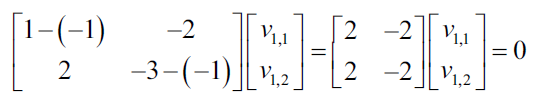
Ahora mostramos las ecuaciones resultantes como un sistema de ecuaciones:

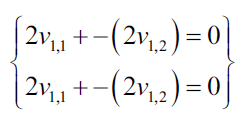
Cada vector no cero que satisface las ecuaciones anteriores, puede ser utilizado como vector propio:

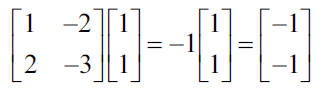
PCA requiere vectores unitarios o vectores que tengan una longitud de 1, Por lo que se pueden normalizar los vectores dividiéndolos por su normal, lo cual se consigue con la siguiente ecuación:

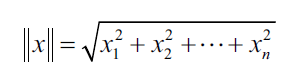
La norma del vector es la siguiente:

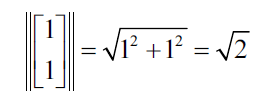
Esto genera el siguiente vector propio unitario:

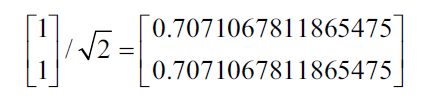
Para verificar con Numpy que la solución anterior sea correcta, podemos hacer lo siguiente donde la función eig regresa una tupla de valores propios  y los vectores propios.

import numpy as np
v, w = np.linalg.eig(np.array([[1, -2], [2, -3]]))

w; v
arrray([-0.99999998, -1.00000002])
array([[0.70710678, 0.70710678], [0.70710678, 0.70710678]])

Reducción de la Dimensionalidad

Utilizando PCA (Principal Component Analysis) para reducir el siguiente conjunto de datos de dos dimensiones en sólo una dimensión:

x1	x2
0.9	1
2.4	2.6
1.2	1.7
0.5	0.7
0.3	0.7
1.8	1.4
0.5	0.6
0.3	0.6
2.5	2.6
1.3	1.1

El primer paso es restar la media de cada variable en cada uno de los casos

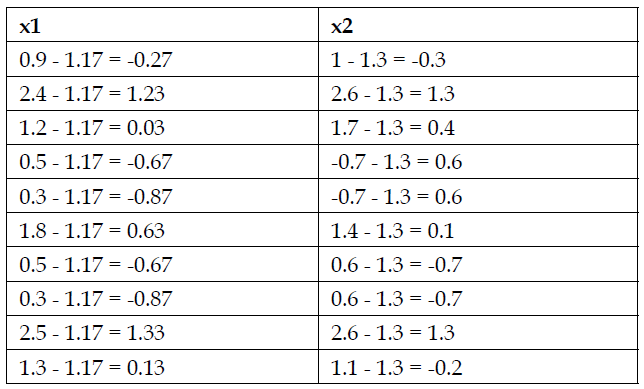
Ahora calculamos los componentes principales de los datos. Recordando que los componentes principales son los vectores propios de la matriz de covarianza ordenada por los valores propios.

Los componentes principales se pueden encontrar utilizando dos técnicas diferentes. La primera técnica requiere calcular la matriz de covarianza de los datos. Dado que la matriz de covarianza será una matriz cuadrada, podemos calcular los vectores y los valores propios como se describió anteriormente. 

La segunda técnica utiliza la descomposición del valor singular de la matriz de datos para encontrar los vectores y la raíz cuadrada de los valores propios de la matriz de covarianza. Utilizamos la primera técnia para describir el proceso y la segunda técnica con la librería scikit-learn.

La siguiente matriz es la matriz de covarianza de los datos

Utilizando la técnica descrita anteriormente, los valores propios son 1.250 y 0.034. La siguiente matriz representa los vectores propios unitarios:

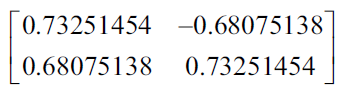
Ahora proyectamos los datos en los componentes principales. El primer vector propio tiene los valores propios más altos y es el primer componente principal. Construimos una matriz de transformación en donde cada columna de la matriz es el vector propio para un componente principal.

Si se estuviera reduciendo un conjunto de datos de 5 dimensiones en un conjunto de tres dimensiones, se construiría una matriz de transformación con 3 columnas. En este ejemplo, proyectamos el conjunto de datos de dos dimensiones en una dimensión, por lo que sólo utilizamos el vector propio para el primer componente principal.

Finalmente calculamos el producto punto de la matriz de datos con la matriz de transformación, resultando lo siguiente:

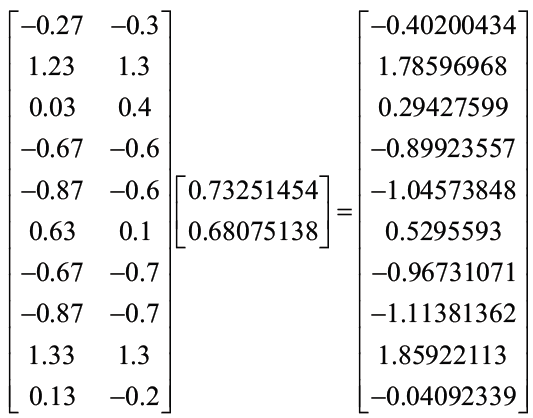
El vector resultante es la dimensión resultante, es decir, es la matriz de una dimensión que corresponde a la variable que resulta de reducir las dos dimensiones originales en una dimensión del conjunto de datos.

PCA con Python

Ahora implementaremos el análisis de componente principal con python, aunque quizás antes de continuare podría ser conveniente que revisaras algunos de los curso de programación que te podrían ayudar a entender la estructura y la lógica detrás de los lenguajes más comunes.

Como primer paso importamos las librerías necesarias para machine learning

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Para este ejemplo utilizaremos un conjunto de datos de una colección de vinos con 13 variables independientes y una variable dependiente, que nos da la clasificación del vino. Las variables independientes son valores característicos del vino en cuestión y que van desde el alcohol, el aroma, el sabor, la acidez, y otros componentes o ingredientes que clasifican un vino.

# Importamos el conjunto de datos
dataset = pd.read_csv('Wine.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values

El conjunto de 177 casos con 13 variables independientes es el siguiente:

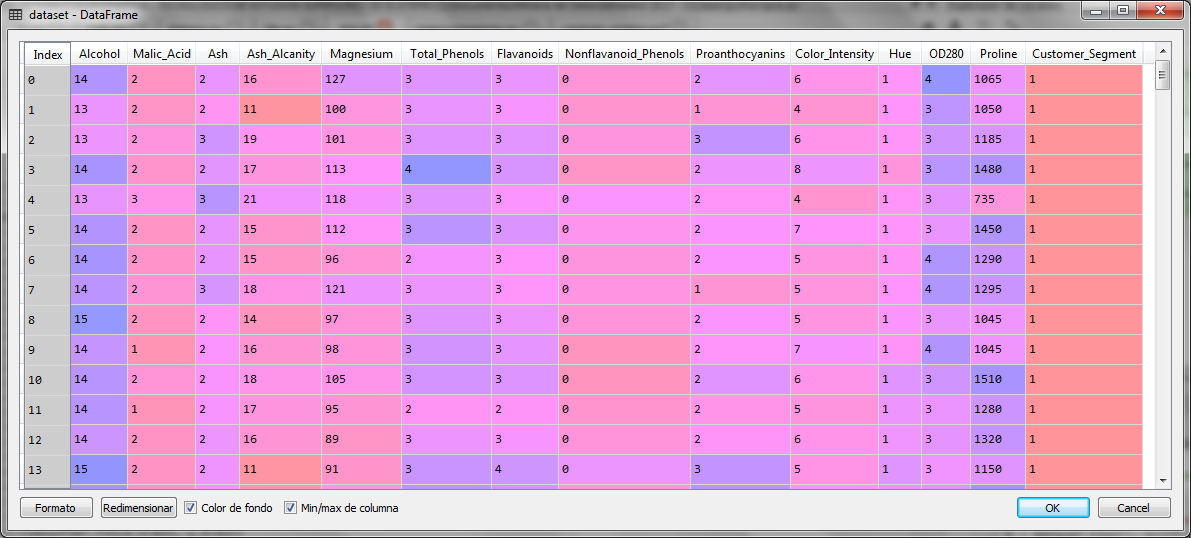
Una vez que importamos los datos, separamos las variables independientes en la matriz X y la variable dependiente en el vector y.

Ahora dividimos el conjunto de datos en dos conjuntos para entrenamiento y prueba

# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)

Nuestro siguiente paso será estandarizar las escalas para las 13 variables

# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

Una vez con los datos normalizados, aplicamos el PCA para reducir la dimensión de 13 a 2 variables.

# Applying PCA
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)

El conjunto de entrenamiento quedó ahora con 2 variables de la siguiente manera:

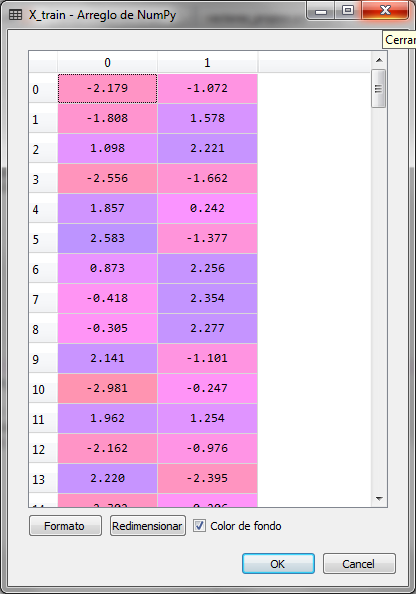
Lo mismo sucedió con el conjunto de pruebas X_test. Ahora para saber que tanto se expresa la varianza de los dos componentes principales resultantes, con relación a la dimensión original, es decir, a los datos de las 13 variables originales, podemos extraer esa información del objeto PCA y analizarla.

# Explicación de la varianza
# Creamos un vector con el porcentaje de influencia de la varianza 
# para las dos variables resultantes del conjunto de datos
explained_variance = pca.explained_variance_ratio_

Los valores de la variable explained_variance son:

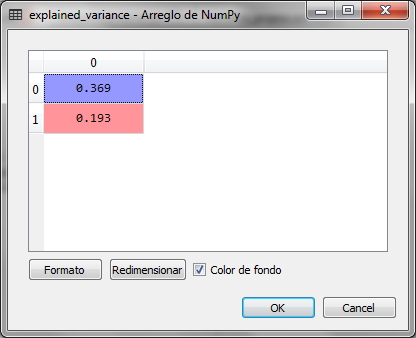
Los dos componentes principales resultantes son los dos valores propios de los vectores propios con el valor más alto de los 13 originales del conjunto de datos. De ahí se obtuvieron los dos más altos para obtener las dos dimensiones resultantes o componentes principales. El primero representa el 36.9%  y el segundo el 19.3%

Para comprobar que las dos variables resultantes representan a las 13 variables originales vamos a hacer la predicción de la variable dependiente con la regresión logística, comprobando los resultados de predicción con la matriz de confusión:

# Fitting Logistic Regression to the Training set
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

# Predicting the Test set results
y_pred = classifier.predict(X_test)

# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

Al hacer la predicción para el conjunto de prueba, la matriz de confusión es la siguiente:

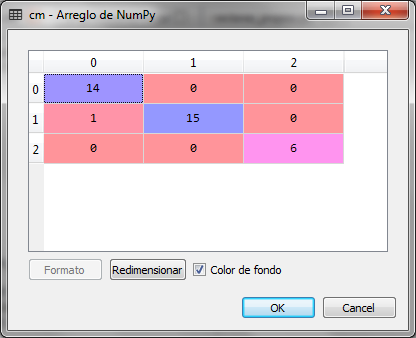
Como se observa en la matriz de confusión, sólo hay un error, un falso positivo en la primera de las tres clases de vinos. Por lo que concluimos que la predicción es correcta utilizando el conjunto de datos de dos variables, en lugar del conjunto de datos de 13 variables.

Ahora podemos graficar los datos de predicción para observar de manera visual los resultados de dicha clasificación

from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()

La gráfica resultante es la siguiente

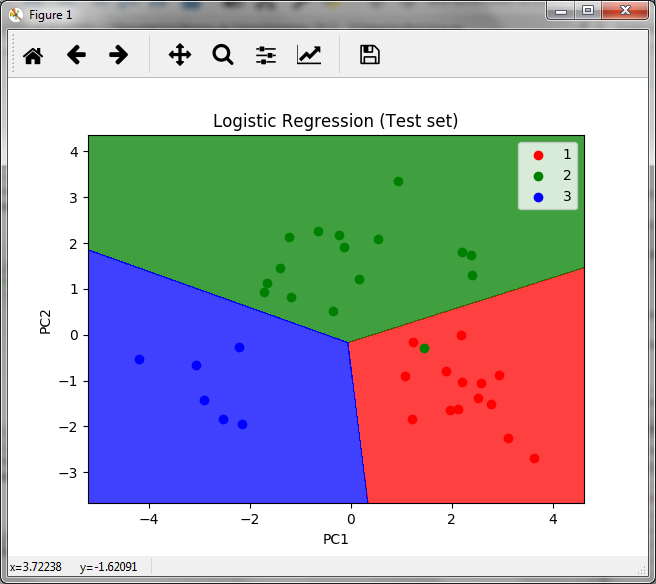
En la gráfica observamos las áreas de las 3 clases de vinos con los puntos de las predicción del conjunto de pruebas, donde además observamos el único error que existe, el punto verde en la zona roja.

Comentarios finales

Muchas veces es necesario implementar este tipo de ejemplos en la nube con una mayor cantidad de datos reales y ejecutar varias de las técnicas y algoritmos de machine learning para realizar algunos comparativos con los distintos algoritmos de clasificación y/o predicción. Hoy en día existe diversos proveedores de recursos en la nube para ciencia de datos y machine learning, algunos de ellos podrían ser: Azure de Microsoft, Alibaba Cloud, Amazon Web Services, en el este enlace puede checar un webinar para conocer las diferentes certificaciones de Azure.

Por otro lado, algunos cursos con buenos descuentos para servicios en la nube los puede checar en Alibaba, donde además podrás verificar información sobre los distintos servicios.

Puedes probar también con los trials sin costo por tiempo suficiente para hacer todo tipo de pruebas.

Por último, siempre será importante contar con las bases de la programación y el manejo de bases de datos, por lo que aquí podrías encontrar algunos cursos interesantes.

Si te interesa el artículo compártelo