Pre-procesamiento de datos
Hoy en día disponemos de una gran cantidad de datos generados por diferentes fuentes y se vuelve cada vez más necesario poder analizarlos ordenadamente para extraer de forma automatizada toda la inteligencia contenida en ellos.
Las técnicas especializadas enfocadas al análisis de datos, constituyen tanto métodos estadísticos como métodos de inteligencia artificial y machine learning, entre otros.
Ve este artículo en video
En este sentido, la minería de datos en sí, es un conjunto de técnicas encaminadas al descubrimiento de la información contenida en grandes conjuntos de datos.
La palabra descubrimiento esta relacionada con el hecho de que mucha de la información valiosa es desconocida con anterioridad, se trata de analizar comportamientos, patrones, tendencias, asociaciones y otras características del conocimiento inmerso en los datos.
El proceso de análisis de datos o data science consta de varias fases:
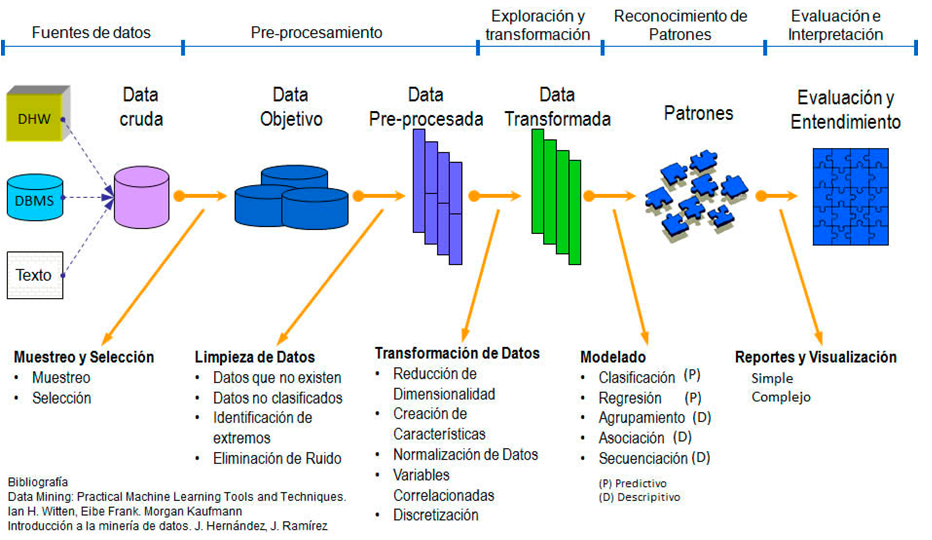
El pre-procesamiento es una estandarización de los datos previo al modelo de análisis y éste consta a su vez de varias fases como se observa en la figura anterior.
Las fases de Selección, Exploración, Limpieza y Transformación conforman el pre-procesamiento de los datos necesario en muchas ocasiones, antes de aplicar algún modelo de análisis de datos, ya sea predictivo o descriptivo.
Muestreo y Selección
En la fase de selección se identifican y seleccionan las variables relevantes en los datos, la variables que nos van a aportar la información para el tema en el que estamos trabajando, así como las fuentes que pueden ser útiles. Una vez seleccionadas las variables se aplican técnicas de muestreo adecuadas con el fin de obtener una muestra de los datos que sea lo suficientemente representativa de la población.
La muestra permite inferir las propiedades o características de toda la población con un error medible y acotable.
A partir de la muestra se estiman las características poblacionales (media, total, proporción, etc.) con un error cuantificable y controlable.
Los errores se cuantifican mediante la varianza, la desviación estándar o el cálculo del error cuadrático medio para obtener la precisión de los errores.
Es importante tomar en cuenta que para obtener el grado de representatividad de la muestra es necesario utilizar muestreo probabilístico.
Exploración
Dado que los datos provienen de diferentes fuentes, es necesaria su exploración mediante técnicas de análisis exploratorio para identificar valores inusuales, valores extremos, valores desaparecidos, discontinuidades u otras peculiaridades de los mismos.
Con ello la fase de exploración ayuda a determinar si son adecuadas las técnicas de análisis de datos que se tienen en consideración. Por ello es necesario realizar un análisis previo de la información de que se dispone antes del uso de cualquier técnica.
Hay que examinar las variables individuales y las relaciones entre ellas, así como evaluar y solucionar problemas en el diseño de la investigación y la recolección de datos.
La exploración puede indicar la necesidad de transformar los datos si la técnica necesita una distribución normal o si se necesita utilizar pruebas no paramétricas.
Para el análisis exploratorio se cuenta con técnicas formales y técnicas gráficas o visuales
Limpieza
Dado que en el conjunto de datos puede haber valores atípicos, valores faltantes y/o valores erroneos, la limpieza de los mismo es importante para solventar alguno de estos inconvenientes. Esta fase es consecuencia del análisis exploratorio.
Transformación
La transformación de los datos es necesaria cuando entre las variables existen diferentes escalas o existen demasiadas o pocas variables, entonces se realiza una normalización o una estandarización de los datos mediante técnicas de reducción o aumento de la dimensión, así como el escalamiento simple o multidimensional.
Si en el análisis exploratorio se indica la necesidad de transformar algunas variables, se podrán aplicar algunas de estas cuatro transformaciones:
- Transformaciones lógicas
- Transformaciones lineales
- Transformaciones algebraicas
- Transformaciones no lineales
Estas fases mencionadas en los puntos anteriores, constituyen el proceso de pre-procesamiento de los datos y para aplicar estos conceptos, se presenta el siguiente ejemplo:
Ejemplo de Pre-procesamiento
Supongamos la siguiente tabla de datos, que representa información de una tienda que relacionó datos de clientes que compraron y clientes que no compraron:
| No | País | Edad | Salario | Compra |
| 1 | Francia | 44 | 72000 | No |
| 2 | España | 27 | 48000 | Si |
| 3 | Alemania | 30 | 54000 | No |
| 4 | España | 38 | 61000 | No |
| 5 | Alemania | 40 | Si | |
| 6 | Francia | 35 | 58000 | Si |
| 7 | España | 52000 | No | |
| 8 | Francia | 48 | 79000 | Si |
| 9 | Alemania | 50 | 83000 | No |
| 10 | Francia | 37 | 67000 | Si |
Como podemos observar, existen registros con datos faltantes. El cliente del registro o renglón 5 no tiene salario y el cliente del renglón 7 no tiene edad.
Cuando se tienen datos faltantes, hay varias estrategias que se pueden seguir, sobre todo si se ha comprobado la aleatoriedad de dichos datos ausentes. Una estrategia es usar el método de aproximación de casos completos que consiste en incluir en el análisis sólo los casos con datos completos, únicamente filas cuyos valores para todas las variables son válidos.
En este caso tenemos que validar si la muestra se ve afectada o no al eliminar los casos incompletos.
La alternativa a los métodos de eliminación de datos es la imputación de la información faltante, donde el objetivo es estimar los valores ausentes basados en valores válidos de otras variables o casos.
Un método para llevar a cabo la imputación de la información faltante es el método de sustitución de casos. Este consiste en sustituir los datos ausentes con datos de observaciones no muestrales, es decir, que no pertenecen a la muestra.
El método de sustitución por la media o la mediana, sustituye los datos ausentes por el valor de la media o la mediana de todos los valores válidos de su variable correspondiente. Cuando existen valores extremos o atípicos, los datos ausentes se sustituyen por la mediana, en caso contrario se utiliza la media.
El método de imputación por interpolación sustituye cada valor ausente por la media o la mediana de un cierto número de datos u observaciones adyacentes a el, sobre todo cuando hay demasiada variabilidad en los datos. Si no existe dicha variabilidad, entonces se sustituyen por el valor resultante de realizar una interpolación con los valores adyacentes.
Adicionalmente, también existe el método de sustitución por un valor constante y como su nombre lo indica, los datos ausentes se sustituyen por un valor constante, válido para la variable en cuestión, derivado de fuentes externas o de una investigación previa.
Por último, podemos utilizar también el método de imputación por regresión y éste utiliza el método de la regresión para calcular o estimar los valores ausentes basados en su relación con otras variables del conjunto de datos.
En nuestro ejemplo vamos a utilizar la media como valor para imputar los datos faltantes tanto de edad como de salario. En este sentido el promedio de valores de la edad es: 38.77 y para el salario, el valor promedio de los valores presentes en la muestra es: 63,777.77, por lo que la tabla ahora queda de la siguiente manera:
| No | País | Edad | Salario | Compra |
| 1 | Francia | 44 | 72000 | No |
| 2 | España | 27 | 48000 | Si |
| 3 | Alemania | 30 | 54000 | No |
| 4 | España | 38 | 61000 | No |
| 5 | Alemania | 40 | 63777.77 | Si |
| 6 | Francia | 35 | 58000 | Si |
| 7 | España | 38.77 | 52000 | No |
| 8 | Francia | 48 | 79000 | Si |
| 9 | Alemania | 50 | 83000 | No |
| 10 | Francia | 37 | 67000 | Si |
Ya tenemos la muestra completa y ahora continuamos con las variables categóricas (País y Compra).
Para la variable Compra, que tiene valores categóricos Si o No, podemos codificarla como 1 y 0 representando 1 para el valor Si y 0 para el valor No. Para el caso de la variable País, el caso es un poco distinto dado que si codificamos como 0, 1 y 2, el país con el valor 2 tendría más peso que el país con el valor 0 por lo que la estrategia para este tipo de variables es diferente.
Dentro de las transformaciones lógicas, las variables de intervalo se pueden convertir en ordinales como las variables Talla o en nominales como Color, y crear variables ficticias o dummy.
| País | Francia | España | Alemania | |
| Francia | 1 | 0 | 0 | |
| España | 0 | 1 | 0 | |
| Alemania | 0 | 0 | 1 |
La variable País la cambiamos por tres variables (Dummy) que son los valores de la variable País. En lugar de utilizar la variable País, utilizamos ahora las 3 variables nuevas y la tabla quedaría de la siguiente forma:
| No | Francia | España | Alemania | Edad | Salario | Compra |
| 1 | 1 | 0 | 0 | 44 | 72000 | 0 |
| 2 | 0 | 1 | 0 | 27 | 48000 | 1 |
| 3 | 0 | 0 | 1 | 30 | 54000 | 0 |
| 4 | 0 | 1 | 0 | 38 | 61000 | 0 |
| 5 | 0 | 0 | 1 | 40 | 63777.77 | 1 |
| 6 | 1 | 0 | 0 | 35 | 58000 | 1 |
| 7 | 0 | 1 | 0 | 38.77 | 52000 | 0 |
| 8 | 1 | 0 | 0 | 48 | 79000 | 1 |
| 9 | 0 | 0 | 1 | 50 | 83000 | 0 |
| 10 | 1 | 0 | 0 | 37 | 67000 | 1 |
Dado que los datos de edad y salario mantienen una escala diferente y en las ecuaciones de la regresión o de algún otro método de clasificación y/o predicción, dada la distancia euclidiana entre dos puntos, el valor del salario podría hacer que la edad deje de ser representativa o importante para el análisis, lo mas conveniente es hacer una transformación de escalas, ya sea una estandarización o una normalización de los datos.

Para este ejemplo usaremos la normalización para ajustar las escalas de todas las variables que está dado por el valor actual de la muestra menos el valor mínimo de todo el conjunto de datos de esa variable entre la diferencia del valor máximo y el valor mínimo.
Una vez aplicada la normalización, la tabla resultante es la siguiente:
| Francia | Alemania | España | Age | Salary | Purchased |
| 1 | 0 | 0 | 0.72003861 | 0.71101283 | 0 |
| 0 | 0 | 1 | -1.62356783 | -1.36437577 | 1 |
| 0 | 1 | 0 | -1.20999022 | -0.84552862 | 0 |
| 0 | 0 | 1 | -0.1071166 | -0.24020695 | 0 |
| 0 | 1 | 0 | 0.1686018 | -6.0532E-07 | 1 |
| 1 | 0 | 0 | -0.52069421 | -0.49963052 | 1 |
| 0 | 0 | 1 | -0.00096501 | -1.01847767 | 0 |
| 1 | 0 | 0 | 1.27147542 | 1.3163345 | 1 |
| 0 | 1 | 0 | 1.54719383 | 1.6622326 | 0 |
| 1 | 0 | 0 | -0.2449758 | 0.2786402 | 1 |
Cuando las variables categóricas generan muchas variables dummy podemos utilizar las técnicas de reducción de la dimensión para hace nuestro conjunto de datos más manejable.
Pre-procesamiento con Python
Utilizando python para realizar el pre-procesamiento del ejemplo anterior se vuelve sencillo con las librerías de numpy y sklearn dado que el subpaquete preprocessing contiene las clases necesarias para realizar la imputación de datos ausentes, la codificación de las variables categóricas, la creación de variables dummy y el ajuste de escalas.
El primer paso es importar las librerías que vamos a utilizar en procesamiento, posteriormente cargamos el conjunto de datos y lo almacenamos en la variable dataset, dividimos la matriz en x (variables independientes) y Y(variable dependiente)
#Pre-procesamiento de datos import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Preproc_Datos_Compras.csv')
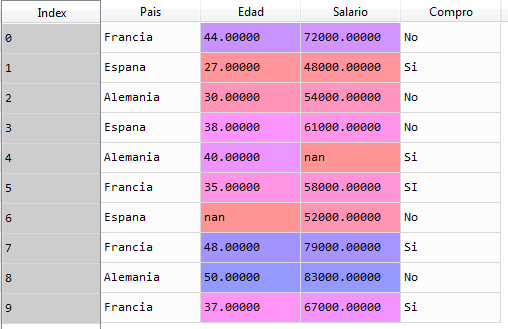
El dataset cargado queda de la siguiente manera y como podemos observar, los datos ausentes se muestran como nan (not a number):
Ahora dividimos las variables en dependientes e independientes
#Pre-procesamiento de datos import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Preproc_Datos_Compras.csv') # Separamos las variables dependientes e independientes x = dataset.iloc[:, :-1] y = dataset.iloc[:, 3]
Al ejecutar este último fragmento de código tenemos las variables x y y
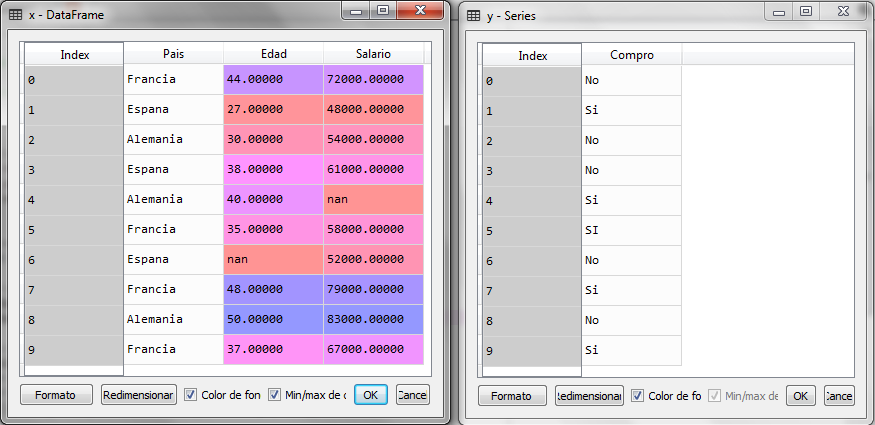
Vemos que en la matriz x, los datos ausentes se muestran como nan (Not an Object). El siguiente paso ahora es la imputación de los datos ausentes y para ello, podemos utilizar la clase Imputer del subpaquete preprocessing.
#Pre-procesamiento de datos import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Preproc_Datos_Compras.csv') # Separamos las variables dependientes e independientes x = dataset.iloc[:, :-1] y = dataset.iloc[:, 3] #Imputacion de datos faltantes from sklearn.preprocessing import Imputer imputer = Imputer(missing_values='NaN', strategy='mean', axis=0) imputer = imputer.fit(x.values[:, 1:3]) x.iloc[:, 1:3] = imputer.transform(x.values[:, 1:3])
Una vez ejecutado el fragmento del código de la clase Imputer, observamos que los datos faltantes se calcularon con la media, que es la estrategia que se le indicó en los argumentos del constructor de la clase Imputer.
El valor promedio de la edad fué 38.77778 y el valor promedio del salario fué 63,777.77778. El siguiente paso es la codificación de las variables categóricas. Primero lo haremos para Y, con los valores Si y No y posteriormente para X con los valores de los países.
#Pre-procesamiento de datos import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Preproc_Datos_Compras.csv') # Separamos las variables dependientes e independientes x = dataset.iloc[:, :-1] y = dataset.iloc[:, 3] #Imputacion de datos faltantes from sklearn.preprocessing import Imputer imputer = Imputer(missing_values='NaN', strategy='mean', axis=0) imputer = imputer.fit(x.values[:, 1:3]) x.iloc[:, 1:3] = imputer.transform(x.values[:, 1:3]) # Codificacion de variables categoricas from sklearn.preprocessing import LabelEncoder label_encoder_y = LabelEncoder() y = label_encoder_y.fit_transform(y) label_encoder_x = LabelEncoder() x.iloc[:, 0] = label_encoder_x.fit_transform(x.values[:, 0]) from sklearn.preprocessing import OneHotEncoder onehotencoder = OneHotEncoder(categorical_features = [0]) x = onehotencoder.fit_transform(x).toarray()
La clase LabelEncoder codifica los valores de Y en 0 para No y 1 para Si, para los países los codifica en 0 Francia, 1 España y 2 Alemanaia, posteriormente la clases OneHotEncoder realiza la transformación de las variables dummy quedando de la siguiente manera:
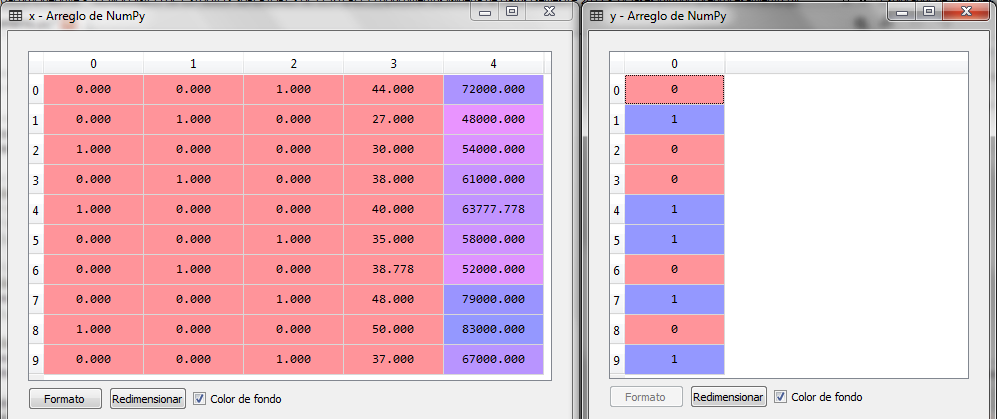
Por último, sólo hace falta la transformación de escalas para las variables de Edad y Salario.
#Pre-procesamiento de datos import numpy as np import matplotlib.pyplot as plt import pandas as pd #Cargamos el conjunto de datos dataset = pd.read_csv('Preproc_Datos_Compras.csv') # Separamos las variables dependientes e independientes x = dataset.iloc[:, :-1] y = dataset.iloc[:, 3] #Imputacion de datos faltantes from sklearn.preprocessing import Imputer imputer = Imputer(missing_values='NaN', strategy='mean', axis=0) imputer = imputer.fit(x.values[:, 1:3]) x.iloc[:, 1:3] = imputer.transform(x.values[:, 1:3]) # Codificacion de variables categoricas from sklearn.preprocessing import LabelEncoder label_encoder_y = LabelEncoder() y = label_encoder_y.fit_transform(y) label_encoder_x = LabelEncoder() x.iloc[:, 0] = label_encoder_x.fit_transform(x.values[:, 0]) from sklearn.preprocessing import OneHotEncoder onehotencoder = OneHotEncoder(categorical_features = [0]) x = onehotencoder.fit_transform(x).toarray() # Transformación de escalas from sklearn.preprocessing import StandardScaler sc_x = StandardScaler() sc_y = StandardScaler() x = sc_x.fit_transform(x) y = sc_y.fit_transform(y.reshape(-1, 1))
Aplicamos la transformación de escalas tanto para las variables del conjunto X como para la variable dependiente Y y vemos que ahora el si es 1 y el no es -1 para estandarizar todos los valores de todas las variables.
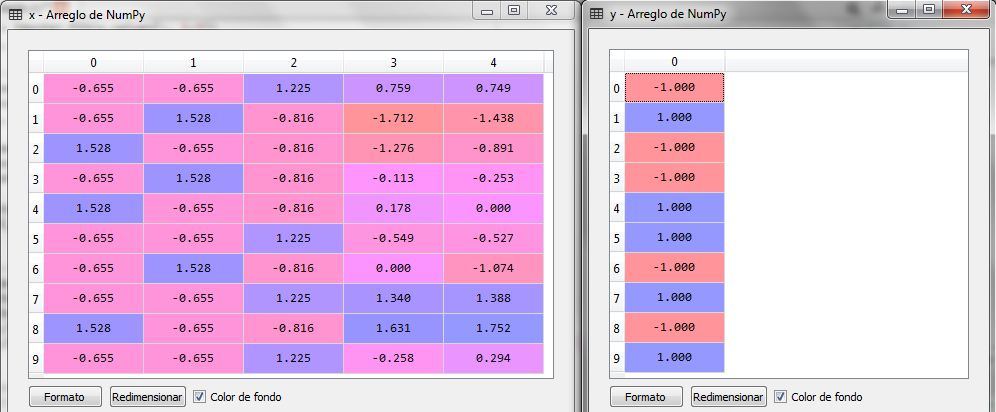
Ahora, ya con los datos pre-procesados podemos aplicar algún método predictivo como la Regresión Logística para predecir las compras de algún cliente nuevo, es decir con sus datos en país, edad y salario, estimar si comprará o no.
Ve este artículo en video
En los siguientes artículos presentaremos métodos de clasificación y predicción.
Si te interesa ahondar más sobre estos temas, tenemos el curso de Python para Ciencia de Datos, checa aquí los detalles
Otro curso muy interesante para iniciar con python lo puedes ver aquí
Para los fundamentos de programación, recomendamos el siguiente curso: Introducción a la programación
Por otro lado, para conocer los detalles para utilizar servicios en la nube con AWS, este curso sobre la certificación de Asociado es bastante recomendable, así como el curso de la certificación profesional.
Finalmente en este webinar podrás ver los detalles para implementar técnicas de machine learning en Azure
Suscribete al blog para recibir las notificaciones cuando se agreguen nuevos artículos


Como siempre, con todo, verdad profe. Soy Sergio López, del TESE, saludos
Muchas gracias Sergio
Te agradezco por este tutorial es Excelente y mu práctico de seguir
Muchisimas gracias Fernando
Buenas noches Jacob, muy bueno el tutorial, una consulta adicional en caso una de las variables originales tenga valores negativos y positivos, se puede aplicar también la estandarización o hay algun método adicional?. Gracias!!!
Gracias por el tutorial Jacob, una consulta adicional, en caso la variable original tenga valores negativos y positivos también se puede aplicar estandarización, o es recomendable algún otro método?. Saludos
Si, no importa el signo. De hecho en la estandarización o normalización el resultado arroja también números negativos.
Hola,
Si, no hay problema con los números negativos, la estandarización se puede usar, al igual que la normalización. El problema sería si existieran valores atípicos. Por que los mínimos, máximos y la media cambian radicalmente. Pero con valores negativos no sucede.