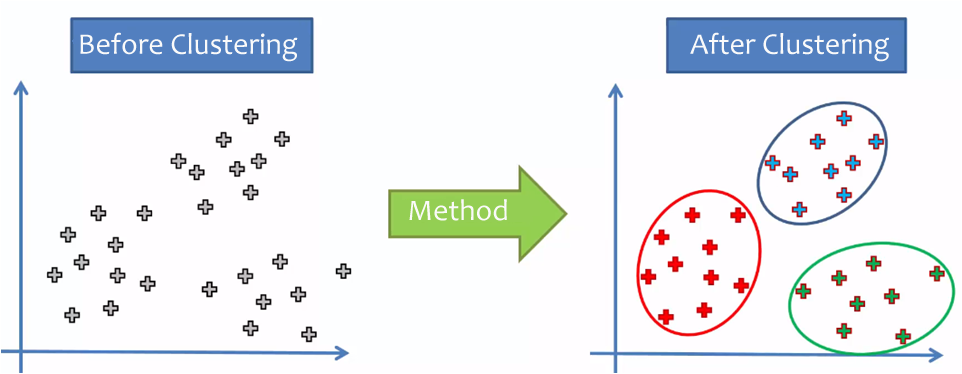
Clustering Analysis

Clustering or conglomerate analysis is a classification and segmentation technique that belongs to the category of unsupervised learning.

Identify groups of subjects that are as heterogeneous as possible and as homogeneous as possible within each group.

The analysis establishes the groups based on the similarity that the entities present with respect to a series of characteristics that were previously specified. So it is the analysis and not the analyst who extracts the groups of subjects and their defining characteristics.

The clustering is a grouping algorithm whose objective is to group data according to a criterion, which usually is distance or similarity.

This similarity is defined in terms of a distance function, such as the Euclidean distance. Although there are other more robust distance functions or that allow to include discrete variables, Euclidean is one of the most accepted. Additionally, the measure most used to validate the similarity between cases is the correlation matrix between the nxn cases.

Its purpose is to reveal concentrations in the data or cases for efficient grouping into clusters or clusters according to their homogeneity and both qualitative variables and quantitative variables can be used, given that the groups are based on proximity or distance from one another.

In this sense, the groups are not known in advance, but perhaps they are suggested by the essence of the data. In other analyzes, such as the case of the discriminant analysis, the groups are previously defined (ad hoc), in the clustering they are not previously specified (post hoc).

Cases and Variables

If the agglomeration variables are at different scales, it will be necessary to standardize or work with deviations from the mean. In the case of missing or missing values, it is suggested to eliminate the cases given that the hierarchical methods have no solution with missing values.

As for the outliers, they deform distances and produce unit clusters. So they must be eliminated from the sample.

If there are correlated variables, a previous multicollinearity analysis or a factorial analysis will be necessary.

On the other hand, the cluster analysis solution does not have to be unique, however, there must be no contradictory solutions when using different grouping methods.

Additionally, the number of observations in each cluster must be relevant and these must have conceptual meaning and not vary much when the sample or agglomeration method changes.

The final groups will be as different as the data allow and with them other analyzes can be made, whether descriptive, discriminant, logistic regression, difference or others.

Clustering methods

As for the grouping methods, there are two general categories:

Hierarchical methods, which can be agglomerative or divisive
Non-hierarchical methods, in which the number of clusters or groups is determined in advance with a prior technique and the cases are assigned to the groups according to their proximity.

The most used methods are sequential, agglomerative, hierarchical and exclusive. In all of them, two fundamental steps are followed in the process of developing the conglomerates:

The first is that the coefficients of similarity or dissimilarity between the new established conglomerates and the potential candidates to be admitted are recalculated at each stage.
and the second, is the criterion of admission of new members to a conglomerate already established.

Hierarchical Methods

In this type of clustering the two most similar clusters are combined until all similar cases are in the same cluster.

There are two main approaches for hierarchical clusters:

Agglomerative or bottom-up (bottom-up) where we take each unit as an individual cluster and combine to form larger clusters
Divisible or from top to bottom (top-down) where it starts with a complete set and they are divided successively into smaller clusters.

Non-hierarchical methods

In the non-hierarchical grouping methods, all the clusters are considered at the same time, since it is required to specify the number of groups that will be generated. The most used non-hierarchical method is the k-Means, which is a model of centroids.

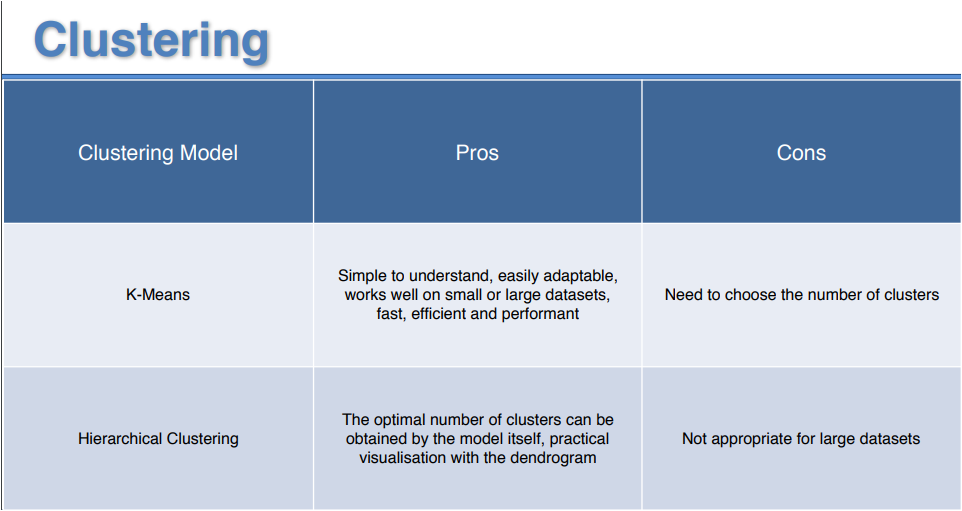
k-Means is a fast, robust and easy to understand method, which makes it relatively efficient if the data is made up of separate and well-separated units. Its main disadvantage is that the value of k is required before starting the algorithm. On the other hand, if the data overlap it will be more difficult to form the clusters.

Another disadvantage is that the method depends on the average and if the data with categorical data, there is no such average and therefore it is not possible to use the k-Means method.

Non-hierarchical methods are more recommended for large amounts of data and are also useful for the detection of atypical cases.

The following articles describe the most commonly used clustering or clustering methods: k-Means and Hierarchical and examples of implementation with Python are presented: